4

I am trying to plot a graph for the Van-der-Waals equation $P=\frac{RT}{V-b}-\frac{a}{V^2} with fixed constants R, T, a, b but definitely there's smth I'm doing wrong. This is my MWE:

 \documentclass[tikz,border=3.14mm]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.17}
\begin{document}
\begin{tikzpicture}[
    declare function={
        R = 8.31;
        T=273;
        a=24.76;
        b=0.02661;
        P(R,T,x, a, b) = (R*T)/(x - b) -(a/x^2);
        P0 = P(8.314, 50, 22.4, 24.76, 0.02661);
  }
    ]

\begin{axis}[
        ytick={0,P0},
        yticklabels={$0$,$P_0$}
        ]
    \addplot[dashed, thick,  domain=0:100]{P(8.314, 50, 22.4, 24.76, 0.02661)};
    \addplot[thick]{P(R,T,x, a, b)};
\end{axis}



\end{tikzpicture}
\end{document}

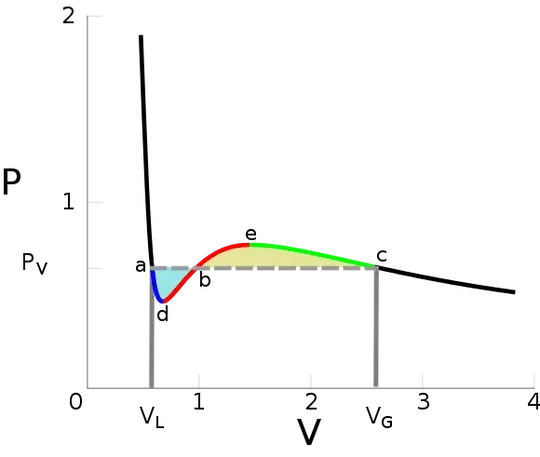
and this is approximately what I want to obtain: enter image description here

I'd be very grateful if someone helped me to figure out my issue

Mirumid
  • 43
  • Welcome to TeX.SX! When defining functions you need to preceed the arguments with a backslash, i.e function P should be defined as P(\R,\T,\x,\a,\b) = (\R*\T)/(\x-\b) - (\a/\x^2); But since R is a constant I would define it as P(\x,\T,\a,\b) = (R*\T)/(\x-\b) - (\a/\x^2);. Doing that allows you to call it as \addplot {P(x,T,a,b)};. Then the remaining part is to find a suitable domain for the volume (here variable x). Good luck. Please share your result when you are successful. – Stefan Pinnow Nov 24 '21 at 10:36

1 Answers1

6

Because it was an interesting question, here a start for your graph. The main point why you most likely failed I did already mention in my comment below the question.

% used PGFPlots v1.18.1
\documentclass[border=5pt]{standalone}
\usepackage{siunitx}
\usepackage{pgfplots}
    \pgfplotsset{compat=1.18}
\begin{document}
\begin{tikzpicture}[
    declare function={
        R=0.083145;     % L bar/(mol K)
        T=573;          % K
        % H2O
        a=5.536;        % L^2/mol^2
        b=0.0305;       % L/mol
        %
        P(\x,\T,\a,\b) = (R*\T)/(\x-\b) - (\a/\x^2);
    },
]
    \begin{axis}[
        xmin=0,
        ymin=0,
        ymax=300,
        enlargelimits=false,
        xlabel=$V_{\mathrm{m}} / \unit{\liter\per\mole}$,
        ylabel=$p / \unit{\bar}$,
        domain=b:1,
        samples=201,
        smooth,
        no markers,
    ]
        \addplot {P(x,T,a,b)};
    \end{axis}
\end{tikzpicture}
\end{document}

image showing the result of above code

Stefan Pinnow
  • 29,535
  • Sir, thank you a lot! – Mirumid Nov 24 '21 at 11:21
  • You are welcome. – Stefan Pinnow Nov 24 '21 at 20:51
  • If this would be my real solution I would further improve it. First would be to use "non-linear spacing" as shown in e.g. https://tex.stackexchange.com/a/373820/95441. This makes sense here, because you only need a lot of points at the beginning of the plot, i.e. for $V_m < 0.2$. The rest can be plotted without any/notable loss with I would say 5 points. – Stefan Pinnow Nov 24 '21 at 21:00