There are three possible strategies for this. I don't recommend what the authors of the paper do (and I'm afraid that their code is not a model to follow), namely \usepackage{MnSymbol}, because this changes all symbols to shapes that are thought to accompany Minion.
One strategy is to use a scaled version of \ominus. Another is to use picture mode. I'll describe instead how to properly import the symbols.
\documentclass{article}
\usepackage{amsmath}
\makeatletter
\newcommand{\bigominus}{\DOTSB\bigominusop\slimits@}
\newcommand{\bigovert}{\DOTSB\bigovertop\slimits@}
\makeatother
\DeclareFontFamily{U}{MnSymbolF}{}
\DeclareFontShape{U}{MnSymbolF}{m}{n}{
<-6> s[1.3] MnSymbolF5
<6-7> s[1.3] MnSymbolF6
<7-8> s[1.3] MnSymbolF7
<8-9> s[1.3] MnSymbolF8
<9-10> s[1.3] MnSymbolF9
<10-12> s[1.3] MnSymbolF10
<12-> s[1.3] MnSymbolF12}{}
\DeclareFontShape{U}{MnSymbolF}{b}{n}{
<-6> s[1.3] MnSymbolF-Bold5
<6-7> s[1.3] MnSymbolF-Bold6
<7-8> s[1.3] MnSymbolF-Bold7
<8-9> s[1.3] MnSymbolF-Bold8
<9-10> s[1.3] MnSymbolF-Bold9
<10-12> s[1.3] MnSymbolF-Bold10
<12-> s[1.3] MnSymbolF-Bold12}{}
\DeclareSymbolFont{MNsymbols}{U}{MnSymbolF}{m}{n}
\SetSymbolFont{MNsymbols}{bold}{U}{MnSymbolF}{b}{n}
\DeclareMathSymbol{\tbigominusop}{\mathop}{MNsymbols}{"36}
\DeclareMathSymbol{\dbigominusop}{\mathop}{MNsymbols}{"37}
\DeclareMathSymbol{\tbigovertop}{\mathop}{MNsymbols}{"38}
\DeclareMathSymbol{\dbigovertop}{\mathop}{MNsymbols}{"39}
\newcommand{\bigominusop}{%
\mathop{\mathchoice{\dbigominusop}{\tbigominusop}{\tbigominusop}{\tbigominusop}}%
}
\newcommand{\bigovertop}{%
\mathop{\mathchoice{\dbigovertop}{\tbigovertop}{\tbigovertop}{\tbigovertop}}%
}
\makeatletter
\newcommand{\cvdots}{%
\vcenter{%
\baselineskip 4\p@
\lineskiplimit \z@
\kern 1\p@
\hbox{.}\hbox{.}\hbox{.}
\kern 1\p@
}%
}
\makeatother
\begin{document}
[
\sum\bigoplus\bigovert\bigominus
\textstyle
\sum\bigoplus\bigovert\bigominus
]
\begin{align}
\left[\begin{array}{c|c|c} A_1 & \dots & A_p \end{array}\right]
&=\bigovert_{1\le j\le p} A_j = \sum_{j=1}^p A_j\cdot \pi_j
\
\left[\begin{array}{@{\quad}c@{\quad}}
A_1 \ \hline \cvdots \ \hline A_m
\end{array}\right]
&=\bigominus_{1\le j\le m} A_j = \sum_{j=1}^m i_j\cdot A_j
\end{align}
\end{document}
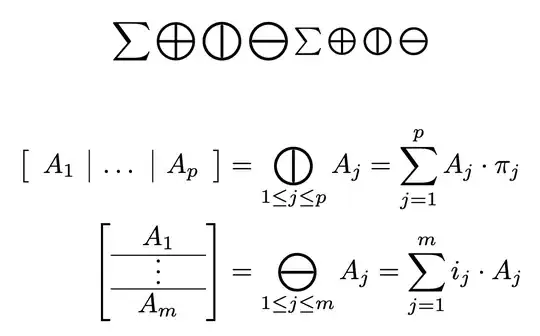
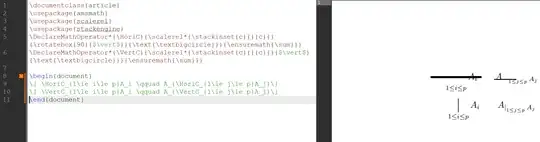
I'm afraid that guessing the code for importing the symbols requires some experience in the job.

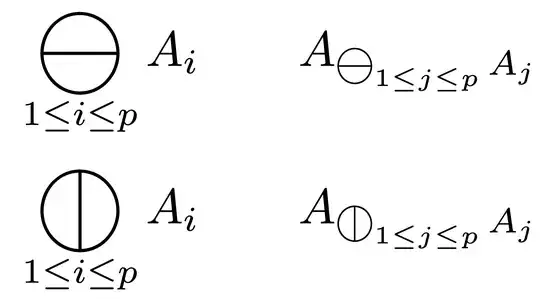
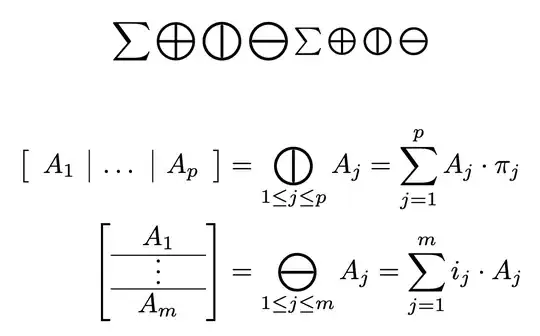
\DeclareMathOperator*command provided by theamsmathpackage. – Nov 25 '21 at 03:50\bigovertand\bigominusfrom the packageMnSymbol. – campa Nov 25 '21 at 08:35