Planes tangent to a cylinder

Question

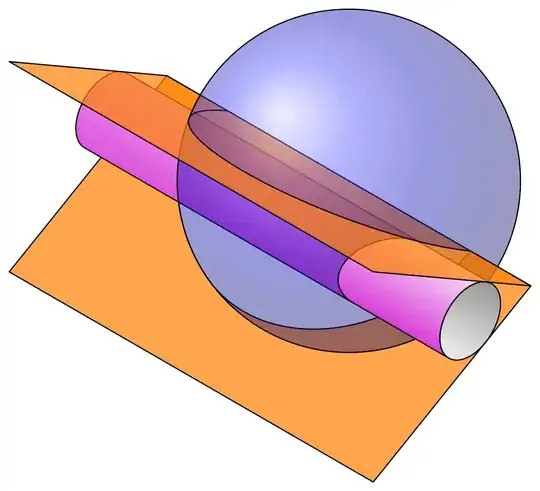
I am trying to make this graph

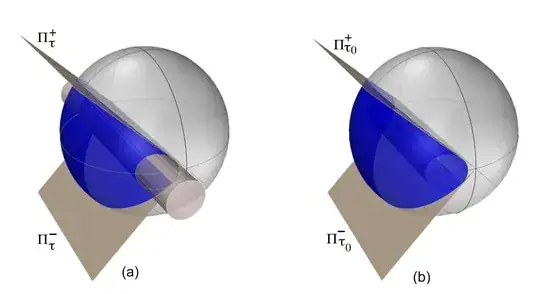
I have had several advances compared to my original question, but I don't know how to color the part blue, This is the result that I have obtained together with the code

settings.render=8;
import three;
import solids;
import bsp;
import graph3;
size (5cm,0);
draw(unitsphere, rgb(0,0.6,0.8) + opacity(.95));
path3 xyplane = path3(scale(1) * box((-1.5,-1.5),(1,0)));
real a=1/(4sqrt(2));
real b=1/(4sqrt(2));
real long=3.3;
real y0=0.28;
real m=180atan(b/sqrt(y0y0-a*a))/pi;
real rotY=4;
real rotZ=65;
real rotXY=-10;
draw(surface(rotate(rotXY,X-Y) * rotate(rotY,Y)rotate(rotZ,Z)rotate(m,X)*xyplane),surfacepen=gray,black + opacity(1));
draw(surface(rotate(rotXY,X-Y) * rotate(rotY,Y)rotate(rotZ,Z)rotate(-m,X)*xyplane),surfacepen=lightgray,black+opacity(1));
surface cylinderSurfaceTiltedPlane(real a, real b, real z0, real y0) {
    triple parametricCylinder(pair p) {
        real Phi = p.x;
        real Z = p.y;
        real x = Z;
        real y = acos(Phi)-y0;
        real z = bsin(Phi);
        return (x,y,z);
    }
    return surface(parametricCylinder, (0,-3z0/4), (2pi,13z0/20), Spline);
}
surface cF =  rotate(rotXY,X-Y) * rotate(rotY,Y)rotate(rotZ,Z)  cylinderSurfaceTiltedPlane(a, b, long, y0);
draw(cF,rgb(255/255,195/255,0/255));
triple f(real t) {
return (cos(t)cos(0), cos(t)sin(0), sin(t));
}
path3 circ = graph(f, 0, 2pi, operator ..);
draw(rotate(rotXY,X-Y) * rotate(75+90,Z)circ,black + 0.1pt);
draw(rotate(rotXY,X-Y)  rotate(75,Z)*circ,black + 0.1pt);
triple g(real t) {
return (cos(t), sin(t),0);
}
path3 cir = graph(g, 0, 2pi, operator ..);
draw(rotate(rotXY,X-Y) * rotate(rotY,Y)rotate(rotZ,Z)cir,black + 0.1pt);

I tried to make it pretty general, since by moving the parameters each one can generate the result you want with the desired perspective. But as I mentioned, I don't know how to do the coloring I have tried to use this:

Code:

import three;
settings.render=8;
size(5cm);
//currentprojection=perspective(50,80,50);
draw(unitsphere, rgb(0,0.6,0.8) + opacity(.95));
triple A=(0.98,-0.17,0.14);
triple MAB=(0,-0.78,0.64); //mid-edge (AB)
triple B=(-0.98,-0.17,0.14);
triple MBC=(-0.89,-0.46,0); //mid-edge
triple C=(-0.98,-0.17,-0.14);
triple MAC=(0,-0.98,0.2); // mid-edge
path3 gc1=(A..MAB..B); //to avoid computation
path3 gc2=(B..(-0.93,-0.33,0.18)..MBC); // I use asymptote path3 routine
path3 gc3=(MBC..MAC..A);
// I recover the different tangents in A, B, C 
// to construct a cycle-path3 of length 3.
path3 gc=point(gc1,0){dir(gc1,0)}..{dir(gc1,2)}point(gc1,2){dir(gc2,0)}
..{dir(gc2,2)}point(gc2,2){dir(gc3,0)}..{dir(gc3,2)}point(gc3,2)..cycle;
draw(surface(patch(gc)),blue);
draw(gc1^^gc2^^gc3);
//dot((gc1^^gc2^^gc3),red);

But as you can see it only covers a part, it is too laborious to calculate the points so that everything goes well, at first I thought about patching it until it comes out, but after a few hours of trying I gave up.

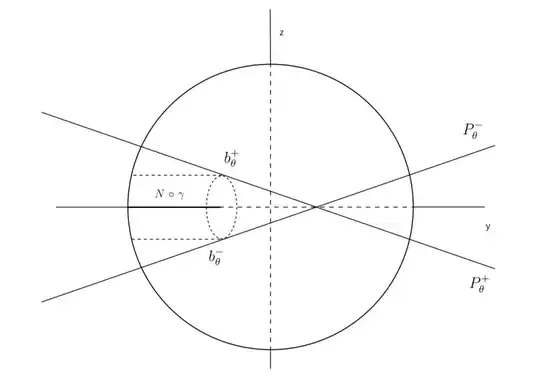
Original question the cylinder must have as its center (*,-1/3,0), in this way the cylinder must be parallel to the x axis. Where the planes are tangent to the cylinder and seen in the yz-plane, we have something like this

Answer 1

Perhaps something like this?

I'm using TikZ 3d and isometric perspective. There are a couple of simplifications. Some points were found by trial-and-error over the sphere (if you see an angle not multiple of 15, that's one of them), because to accurately find them will be quite heavy on the math department. Then, the back curve of intersection between cylinder and sphere lies almost over the sphere border so it's not drawn.

This is the code:

\documentclass[tikz,border=2mm]{standalone}
\usetikzlibrary{3d,perspective}
\tikzset
{
  cylinder/.style={thick,bottom color=magenta!80!black,top color=white,shading angle=-30},
  inside/.style={thick,bottom color=gray!20,top color=gray!80,shading angle=-30},
  sphere/.style={thick,ball color=blue,fill opacity=0.4},
  plane/.style={thick,fill=orange,fill opacity=0.7},
}
\begin{document}
\begin{tikzpicture}[line cap=round,line join=round,
                    isometric view,rotate around z=180,rotate around x=90]
  \pgfmathsetmacro\a{asin(0.5)} % planes angle
  % bottom plane
  \draw[plane] (0,0,-4) {[rotate around z=-\a,canvas is xz plane at y=0] arc (-90:16:4)} --
               (218:4cm) arc (218:150:4cm) -- (0,0,6) --++ (-\a:6) --++ (0,0,-12) -- (0,0,-6) -- cycle;
  % cylinder, back and inside
  \draw[cylinder] (2,0,6) + (135:1) arc (135:-45:1) --
                  ({2+cos(315)},{sin(315)},{-sqrt(11-4cos(315))}) --
                   plot[domain=-45:135,samples=91] ({2+cos(\x)},{sin(\x)},{-sqrt(11-4cos(\x)}) -- cycle;
  % top plane, inside
  \fill[plane] (150:4cm) arc (150:159:4cm)
      {[rotate around z= \a,canvas is xz plane at y=0] arc (54:-90:4)} -- cycle;
  \draw[thick,rotate around z=\a,canvas is xz plane at y=0] (0,4) arc (90:54:4);
  \draw[thick] (150:4cm) -- (0,0,-4);
  % sphere
  \draw[sphere] (0,0,0) circle (4cm);

  % cylinder, front
  \draw[cylinder] (2,0,-6) + (135:1) arc (135:-45:1) --
                  ({2+cos(315)},{sin(315)},{-sqrt(11-4cos(315))}) --
                   plot[domain=-45:135,samples=91] ({2+cos(\x)},{sin(\x)},{-sqrt(11-4cos(\x)}) -- cycle;
  \draw[canvas is xy plane at z=-6,inside] (2,0) circle (1);
  % top plane, outside
  \draw[plane] (150:4cm) -- (0,0,6) --++ (\a:6) --++ (0,0,-12) -- (0,0,-6) -- (0,0,-4)
    {[rotate around z=\a,canvas is xz plane at y=0] arc (-90:54:4)} -- (159:4 cm)  arc (159:150:4cm);
\end{tikzpicture}
\end{document}