I'd like to suggest that you not use a split environment (or its close sibling, the aligned environment). Instead, I'd recommend you employ a multline* environment, especially since the integral expressions vary considerable in width, making it unappealing to employ an align* env.
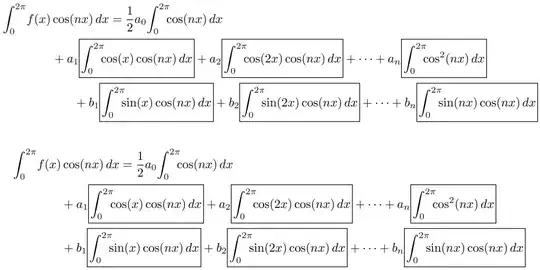
The following screenshots shows solutions that employ a multline* and an align* environment. Note that I've tried to save some (horizontal) whitespace by a triple negative whitespace after all \int terms and changing \boxed{...} to `\boxed{!...!}.
\documentclass{article}
\usepackage[a4paper,margin=2.5cm]{geometry} % set page margins as needed
\usepackage{amsmath}
\begin{document}
\begin{multline*}
\int_{0}^{2\pi}! f(x)\cos(nx),dx
= \frac{1}{2}a_0!\int_{0}^{2\pi}!!!\cos(nx),dx\
- a_1\boxed{!\int_{0}^{2\pi}!!!\cos(x)\cos(nx),dx!}
- a_2 \boxed{!\int_{0}^{2\pi}!!!\cos(2x)\cos(nx),dx!}
- \dots
- a_n\boxed{!\int_{0}^{2\pi}!!!\cos^2(nx),dx!} \
- b_1\boxed{!\int_{0}^{2\pi}!!!\sin(x)\cos(nx),dx!}
- b_2\boxed {!\int_{0}^{2\pi}!!!\sin(2x)\cos(nx),dx!}
- \dots
- b_n\boxed{!\int_{0}^{2\pi}!!!\sin(nx)\cos(nx),dx!}
\end{multline*}
\begin{align*}
\int_{0}^{2\pi}! f(x)&\cos(nx),dx
= \frac{1}{2}a_0!\int_{0}^{2\pi}!!!\cos(nx),dx\
&+ a_1\boxed{!\int_{0}^{2\pi}!!!\cos(x)\cos(nx),dx!}
- a_2 \boxed{!\int_{0}^{2\pi}!!!\cos(2x)\cos(nx),dx!}
- \dots
- a_n\boxed{!\int_{0}^{2\pi}!!!\cos^2(nx),dx!} \
&+ b_1\boxed{!\int_{0}^{2\pi}!!!\sin(x)\cos(nx),dx!}
- b_2\boxed {!\int_{0}^{2\pi}!!!\sin(2x)\cos(nx),dx!}
- \dots
- b_n\boxed{!\int_{0}^{2\pi}!!!\sin(nx)\cos(nx),dx!}
\end{align*}
\end{document}


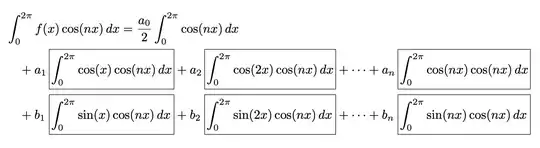
\\and an alignment marker&before both thea_nandb_nterms. Just remove those. (Of course, potentially what you wrote will not fit on one line.) – Willie Wong Jan 23 '22 at 05:32