I found it an interesting challenge, since it is about placing terms in something similar to a spiral, searching I found this very detailed code from Guilherme Zanotelli to draw parametric spirals, and then I adapted it to obtain a similar result, I have used some nesting to place the nodes.
RESULT:
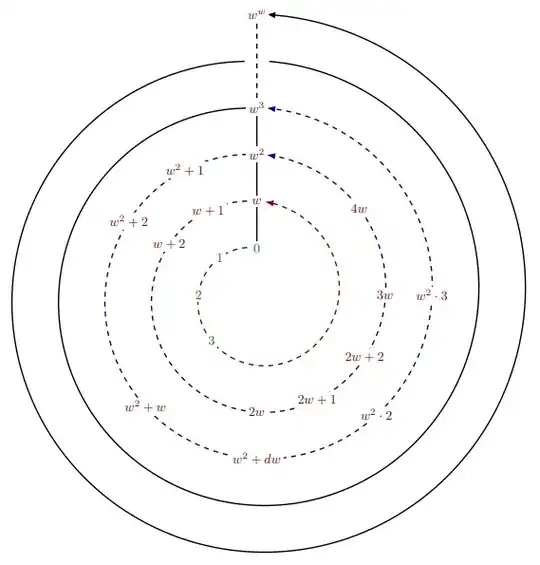
MWE:
\documentclass[tikz,border=0.5cm]{standalone}
%this code is from Guilherme Zanotelli in a "short" explanation in https://tex.stackexchange.com/a/333824/154390 [start]
\newcommand\bonusspiral{} % just for safety
% \bonusspiraldraw options(start angle:end angle)(start radius:final radius)[revolutions]
\def\bonusspiral#1(#3:#4)(#5:#6)[#7]{
\pgfmathsetmacro{\domain}{#4+#7360}
\pgfmathsetmacro{\growth}{180(#6-#5)/(pi(\domain-#3))}
\draw [#1,
shift={(#2)},
domain=#3pi/180:\domainpi/180,
variable=\t,
smooth,
samples=int(\domain/5)] plot ({\t r}: {#5+\growth\t-\growth#3pi/180});
}
%this code is from Guilherme Zanotelli in a "short" explanation in https://tex.stackexchange.com/a/333824/154390 [end]
%Modification to put a node in specific point of the function
%\NodeOnSpiraldraw options(start angle:end angle)(start radius:final radius)[revolutions]{node_position_in_degrees}{node content}
\def\NodeOnSpiral#1(#3:#4)(#5:#6)[#7]#8#9{
\pgfmathsetmacro{\dom}{#4+#7360}
\pgfmathsetmacro{\grow}{180(#6-#5)/(pi(\dom-#3))}
\path [
shift={(#2)},
domain=#3pi/180:\dompi/180,
variable=\j,
smooth,
samples=int(\dom/5),
samples at=#8pi/180
]
plot ({\j r}: {#5+\grow\j-\grow#3*pi/180})
node[
#1,
rectangle,
fill=white,
inner sep=2pt,
scale=0.8
]{#9};
}
\begin{document}
\begin{tikzpicture}[>=latex]
%Start drawing the thing.
% First spiral is used as workspace a spiral that starst from 90 at radious 1 and ends at 90 at radious 6.
\bonusspiralblack!10,dotted, thick(90:90)(1:6)[5]
% Draw a line from (90:1) to (90:6)
\draw[thick] (90:1) -- (90:4);
\draw[thick,dashed] (90:4) -- (90:6);
% Draw the first spiral arrow in one revolution from 90:1 to 85:2. no to 90:2 to not put the arrow interrupting the node
\bonusspiral[red!50!black,dashed, thick,->](0,0)(90:85)(1:2)[1]
% Put the nodes in their corresponding angle position in the spiral.
\foreach \degpos/\nodetext in {
90/0,
135/1,
180/2,
225/3%
}{\NodeOnSpiral[green!50!black](0,0)(90:90)(1:3)[2]{\degpos}{$\nodetext$}}
% Draw the second spiral arrow in one revolution from 90:2 to 85:3.
\bonusspiral[blue!50!black,dashed, thick,->](0,0)(90:86)(2:3)[1]
% same thing in the corresponding spiral and revolution angle.
\foreach \degpos/\nodetext in {
450/w,
480/w+1,
510/w+2,
630/2w,
660/2w+1,
690/2w+2,
720/3w,
760/4w%
}{\NodeOnSpiral[red!50!black](0,0)(90:90)(1:3)[2]{\degpos}{$\nodetext$}}
% Draw the third spiral arrow in one revolution from 90:3 to 85:4.
\bonusspiral[blue!50!black,dashed, thick,->](0,0)(90:87)(3:4)[1]
% same thing in the corresponding spiral and revolution angle.
\foreach \degpos/\nodetext in {
810/w^2,
840/w^2+1,
870/w^2+2,
945/w^2+w,
990/w^2+dw,
1035/w^2\cdot2,
1080/w^2\cdot3%
}{\NodeOnSpiral[red!50!black](0,0)(90:90)(1:3)[2]{\degpos}{$\nodetext$}}
% Draw the last spirals arrow in two revolutions from 95:4 to 88:6.
\bonusspiral[black, thick](0,0)(93:87)(4:5)[1]
\bonusspiral[black, thick,->](0,0)(93:88)(5:6)[1]
% same thing in the corresponding spiral and revolution angle.
\foreach \degpos/\nodetext in {
1170/w^3,
1890/w^w%
}{\NodeOnSpiral[red!50!black](0,0)(90:90)(1:3)[2]{\degpos}{$\nodetext$}}
\end{tikzpicture}
\end{document}
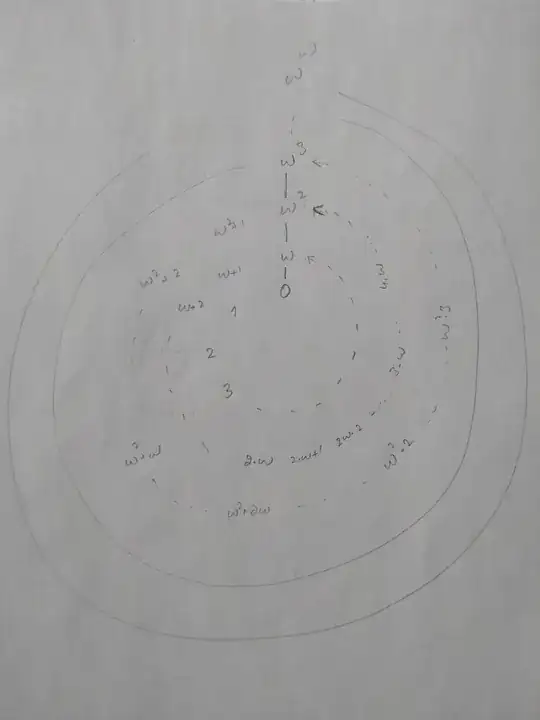
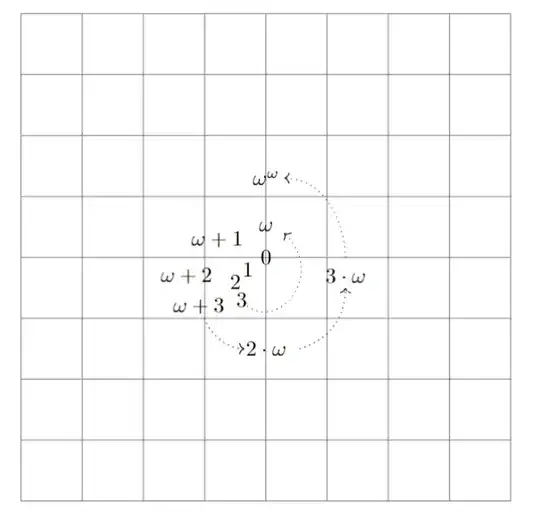

(r:phi)-- note the semi-colon -- where r is the distance to the center, and phi the polar angle (by default in degrees). In the present case, you woukd use an r defined as a linear fiction of phi, in order to produce the spiraling shape. And the size issue could be solved by using globally a smaller font like e.g.,\footnotesize, or increase the canvas size by providing[x=15mm,y=15mm]or similar as a option for the tikz picture. – Jhor Mar 07 '22 at 00:39