4

The following code shows an offset of the calculate point when I use the scale=1.25. I have the possibility to use transform canvas={scale=1.25} with a scope but this leads to other difficulties like the need to create a bounding box manually. This is very annoying because on a complex geometrical construction the shifts can combine and result in a false figure. In general this happens as soon as distance calculations are used. Is there a way to avoid this problem?

\documentclass[landscape]{article} 
\usepackage{tikz,fullpage}
 \usetikzlibrary{calc} 
\begin{document} 
\parindent=0pt

\begin{tikzpicture}
\drawhelp lines grid (18,1);
 \coordinate(A) at (0,0);
 \coordinate(C) at (10,0);
 \coordinate(B) at (6,0);
 \path (A) -- (B) coordinatepos=.5;
 \path (B) -- (C) coordinatepos=.5;
 \path[coordinate] let 
   \p1 = ($ (B) - (E) $),
   \n1={veclen(\x1,\y1)},
   \p2 = ($ (B) - (F) $),
   \n2={veclen(\x2,\y2)},
    in (barycentric cs:E={-\n2/1cm},F={\n1/1cm}) coordinate (D);
 \foreach \point in {A,B,C,D,E,F}
    \fill [black,opacity=.5] (\point) circle (2pt);
\end{tikzpicture}


\vspace{1cm}
\begin{tikzpicture}[scale=1.25]
  \drawhelp lines grid (18,1);
  \coordinate(A) at (0,0);
  \coordinate(C) at (10,0);
  \coordinate(B) at (6,0);
  \path (A) -- (B) coordinatepos=.5;
  \path (B) -- (C) coordinatepos=.5;
  \path[coordinate] let 
    \p1 = ($ (B) - (E) $),
    \n1={veclen(\x1,\y1)},
    \p2 = ($ (B) - (F) $),
    \n2={veclen(\x2,\y2)},
     in (barycentric cs:E={-\n2/1cm},F={\n1/1cm}) coordinate (D);
  \foreach \point in {A,B,C,D,E,F}
     \fill [black,opacity=.5] (\point) circle (2pt);
\end{tikzpicture}


\vspace{1cm}
\begin{tikzpicture}
\begin{scope}[transform canvas={scale=1.25}]
  \drawhelp lines grid (18,1);
  \coordinate(A) at (0,0);
  \coordinate(C) at (10,0);
  \coordinate(B) at (6,0);
  \path (A) -- (B) coordinatepos=.5;
  \path (B) -- (C) coordinatepos=.5;
  \path[coordinate] let 
    \p1 = ($ (B) - (E) $),
    \n1={veclen(\x1,\y1)},
    \p2 = ($ (B) - (F) $),
    \n2={veclen(\x2,\y2)},
     in (barycentric cs:E={-\n2/1cm},F={\n1/1cm}) coordinate (D);
  \foreach \point in {A,B,C,D,E,F}
     \fill [black,opacity=.5] (\point) circle (2pt);
\end{scope}
\useasboundingbox (0,0) rectangle (18,1);
\end{tikzpicture}
\end{document}

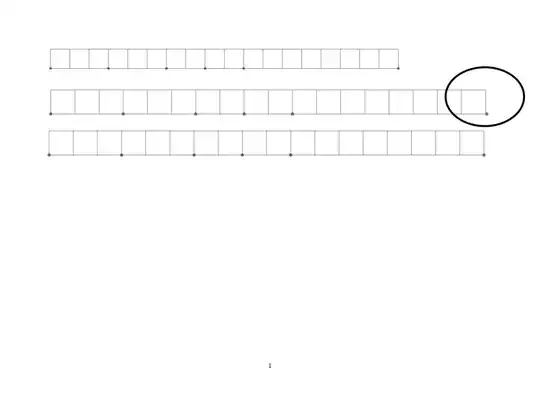
enter image description here

Alain Matthes
  • 95,075
  • @pascal974 Interesting link because I did not know the existence of several macros but unfortunately not because as transform canvas everything is scaled, which I do not want (line thickness, fonts etc.) and the bounding boxis lost. The good way is to improve some calculations, or even to avoid them. The pgf maintainers have given me some ideas. The problem after a scale is that rounding errors are propagated and sometimes their accumulation is a problem. The very good solution would be to do the calculations only with lua. – Alain Matthes Mar 19 '22 at 14:06
  • Sorry, I deleted my comment pretty quickly (I thought), I had seen that it works like transform canvas. I didn't see that you replied. Thank's for your explanation. The link was https://tex.stackexchange.com/questions/4338/correctly-scaling-a-tikzpicture. – pascal974 Mar 20 '22 at 13:00

1 Answers1

1

enter image description here A solution to the problem of propagating errors would be the computation of the barycenter directly (using calc) without invoking the change of coordinates on the canvas.

The code

\documentclass[landscape]{article} 
\usepackage{tikz, fullpage}
 \usetikzlibrary{calc} 
\begin{document} 
\parindent=0pt

Computing $D$ directly as a barycenter of $E$ and $F$\
\begin{tikzpicture}
  \drawhelp lines grid (18,1);
  \coordinate(A) at (0,0);
  \coordinate(C) at (10,0);
  \coordinate(B) at (6,0);
  \path (A) -- (B) coordinatepos=.5;
  \path (B) -- (C) coordinatepos=.5;
  \path[coordinate] let 
    \p1 = ($ (B) - (E) $),
    \n1={veclen(\x1,\y1)},
    \p2 = ($ (B) - (F) $),
    \n2={veclen(\x2,\y2)},
  in (${-\n2/1cm}(E) +{\n1/1cm}(F)$) coordinate (D);
  \foreach \point in {A,B,C,D,E,F}
  \filldraw[blue!70!black, opacity=.5] (\point) circle (2pt)
  node[below right, opacity=1] {$\point$};
\end{tikzpicture}


\vspace{1cm}
Computing $D$ by invoking the barycentric system through
\texttt{barycenter cs:}\
\begin{tikzpicture}
  \drawhelp lines grid (18,1);
  \coordinate(A) at (0,0);
  \coordinate(C) at (10,0);
  \coordinate(B) at (6,0);
  \path (A) -- (B) coordinatepos=.5;
  \path (B) -- (C) coordinatepos=.5;
  \path[coordinate] let 
    \p1 = ($ (B) - (E) $),
    \n1={veclen(\x1,\y1)},
    \p2 = ($ (B) - (F) $),
    \n2={veclen(\x2,\y2)},
  in (barycentric cs:E={-\n2/1cm},F={\n1/1cm}) coordinate (D);
  \foreach \point in {A,B,C,D,E,F}
  \filldraw [black, opacity=.5] (\point) circle (2pt)
  node[below right, opacity=1] {$\point$};
\end{tikzpicture}


\vspace{1.5cm}
Computing $D$ directly as a barycenter of $E$ and $F$ $+$
\texttt{scale=1.25}\
\begin{tikzpicture}[scale=1.25]
  \drawhelp lines grid (18,1);
  \coordinate(A) at (0,0);
  \coordinate(C) at (10,0);
  \coordinate(B) at (6,0);
  \path (A) -- (B) coordinatepos=.5;
  \path (B) -- (C) coordinatepos=.5;
  \path[coordinate] let 
    \p1 = ($ (B) - (E) $),
    \n1={veclen(\x1,\y1)},
    \p2 = ($ (B) - (F) $),
    \n2={veclen(\x2,\y2)},
  in (${-\n2/1cm}(E) +{\n1/1cm}(F)$) coordinate (D);
  \foreach \point in {A,B,C,D,E,F}
  \filldraw [blue!70!black, opacity=.5] (\point) circle (2pt)
  node[below right, opacity=1] {$\point$};
\end{tikzpicture}


\vspace{1cm}
Computing $D$ by invoking the barycentric system through
\texttt{barycenter cs:} $+$ \texttt{scale=1.25}\
\begin{tikzpicture}[scale=1.25]
  \drawhelp lines grid (18,1);
  \coordinate(A) at (0,0);
  \coordinate(C) at (10,0);
  \coordinate(B) at (6,0);
  \path (A) -- (B) coordinatepos=.5;
  \path (B) -- (C) coordinatepos=.5;
  \path[coordinate] let 
    \p1 = ($ (B) - (E) $),
    \n1={veclen(\x1,\y1)},
    \p2 = ($ (B) - (F) $),
    \n2={veclen(\x2,\y2)},
  in (barycentric cs:E={-\n2/1cm},F={\n1/1cm}) coordinate (D);
  \foreach \point in {A,B,C,D,E,F}{
    \filldraw [black,opacity=.5] (\point) circle (2pt)
    node[below right, opacity=1] {$\point$};
  }
\end{tikzpicture}
\end{document}
Daniel N
  • 5,687