Hi guys I wanted to do the following plot using tikz.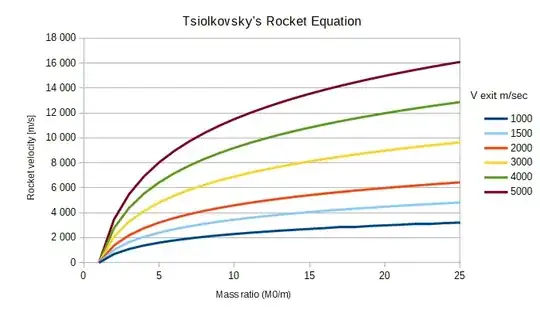
Can you help me replicate this picture? I'd prefer not to use pgfplots instead I'd like to use the \draw plot function. The plotted equation sounds like this $y=v_{exit}ln(M_0/m})$.
Hi guys I wanted to do the following plot using tikz.
Can you help me replicate this picture? I'd prefer not to use pgfplots instead I'd like to use the \draw plot function. The plotted equation sounds like this $y=v_{exit}ln(M_0/m})$.
Here is a TikZ solution.
The actual scale of the graph is from 0 to 5 on the x-axis and 0 to 9 on the y-axis. The labels are calculated accordingly. The xscale and yscale settings are for appearance only, so that the graph is 10cm wide (with xscale set at 2) and 7.2cm high (with y-scale set at .8). Of course you can change the values of xscale and yscale however you like to best fit your document.
\documentclass{article}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}[xscale=2,yscale=.8,font=\sffamily]
\draw[gray!50] (0,9)--(0,0) (-.1,0)node[black,left]{0}--(5,0)--(5,9);
\foreach \y in {2,4,...,18}{\drawgray!50node[black,left]{\y,000}--(5,\y/2);}
\foreach \x in {0,5,...,25}{\drawgray!50node[black,below]{\x}--(\x/5,0);}
\foreach \v/\c[count=\n,evaluate=\v as \l using int(\v1000)]
in {1/red,1.5/orange,2/yellow,3/green,4/blue,5/violet}{
\draw[ultra thick, \c, domain=.2:5, smooth, variable=\x] plot (\x, {.5\vln(5\x)});
\drawultra thick, \c--(5.8,7-\n/1.5)node[black,right]{\l};
}
\end{tikzpicture}
\end{document}
actual scale is from 0 to 5" refers to the physical paper dimensions (cm by default AFAIK) AND the diagram units, correct?
– Dr. Manuel Kuehner
Mar 28 '22 at 04:25
xscale and yscale. I'll try to make my explanation more clear.
– Sandy G
Mar 28 '22 at 04:27
pgfplots.\documentclass[tikz]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.18}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
xlabel = $x$,
ylabel = {$a \cdot \ln(x)$},
xmin = 0,
xmax = 25,
axis x line = bottom,
axis y line = left,
]
% Plot 1
\addplot[
domain = 1:25,
samples = 201,
smooth,
color = blue,
] {10ln(x)};
\addlegendentry{$a = 10$}
% Plot 2
\addplot[
domain = 1:25,
samples = 201,
smooth,
color = red,
] {20ln(x)};
\addlegendentry{$a = 20$}
\end{axis}
\end{tikzpicture}
\end{document}
pgfplotsunless you have a good reason not to. – Dr. Manuel Kuehner Mar 27 '22 at 23:17