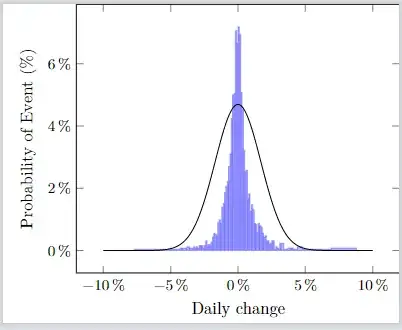
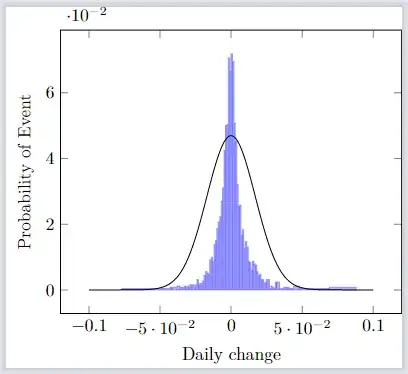
I tried to copy some of the previous solutions for this exact problem, but none worked. I'm not sure why, but possibly because of the interval, in which all of the data is, being too small. Anyways here is my latex file:
\documentclass{standalone}
\usepackage[utf8]{inputenc}
\usepackage[T1]{fontenc}
\usepackage{tikz}
\usepackage{pgfplots}
\begin{document}
\pgfplotsset{scaled y ticks=false}
\begin{tikzpicture}
\begin{axis}
[xlabel={Daily change},ylabel={Probability of Event (%)},
ylabel style={align=center,text width=5cm},
yticklabel=\pgfmathparse{100\tick}\pgfmathprintnumber{\pgfmathresult},%,
xticklabel=\pgfmathparse{100\tick}\pgfmathprintnumber{\pgfmathresult},%,
xticklabel style={font=\small,/pgf/number format/fixed, /pgf/number format/precision=2},
yticklabel style={font=\small}]
\addplot [ybar interval, color=blue,opacity=0.3,fill=blue] table[x=C,y=V]{sp500Dist.dat};
\end{axis}
\end{tikzpicture}
\end{document}
And here is how the output file looks like:
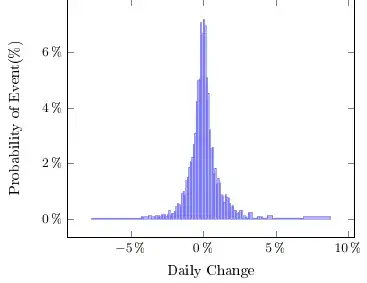
And here is the sp500Dist.dat file
C V
-0.077 0.000397141
-0.063 0.000397141
-0.062 0.000397141
-0.056 0.000397141
-0.052 0.000397141
-0.049 0.000397141
-0.048 0.000397141
-0.047 0.000397141
-0.046 0.000397141
-0.043 0.000794281
-0.042 0.000794281
-0.041 0.000794281
-0.038 0.00119142
-0.036 0.000794281
-0.034 0.000794281
-0.033 0.00119142
-0.032 0.000794281
-0.031 0.00119142
-0.03 0.000794281
-0.029 0.00158856
-0.028 0.00158856
-0.027 0.00158856
-0.026 0.000794281
-0.025 0.00158856
-0.024 0.00317712
-0.023 0.00158856
-0.022 0.0019857
-0.021 0.0019857
-0.02 0.00277998
-0.019 0.00436855
-0.018 0.00555997
-0.017 0.00516283
-0.016 0.00476569
-0.015 0.00913423
-0.014 0.00992851
-0.013 0.00873709
-0.012 0.0138999
-0.011 0.0150913
-0.01 0.0186656
-0.009 0.0206513
-0.008 0.0222399
-0.007 0.0270056
-0.006 0.030977
-0.005 0.042494
-0.004 0.0500397
-0.003 0.0504369
-0.002 0.070691
-0.001 0.0667196
0 0.0718824
0.001 0.0694996
0.002 0.050834
0.003 0.045274
0.004 0.0321684
0.005 0.025417
0.006 0.0258141
0.007 0.0166799
0.008 0.0182685
0.009 0.0127085
0.01 0.0146942
0.011 0.0131056
0.012 0.00873709
0.013 0.00833995
0.014 0.00595711
0.015 0.00873709
0.016 0.00794281
0.017 0.00754567
0.018 0.00555997
0.019 0.00436855
0.02 0.00476569
0.021 0.00317712
0.022 0.00317712
0.023 0.0019857
0.024 0.00238284
0.025 0.00317712
0.026 0.00317712
0.027 0.000397141
0.028 0.00119142
0.029 0.000794281
0.03 0.000397141
0.031 0.00238284
0.032 0.00238284
0.034 0.000397141
0.036 0.000397141
0.037 0.000794281
0.039 0.000794281
0.04 0.000794281
0.041 0.000397141
0.042 0.000397141
0.044 0.00119142
0.048 0.000397141
0.049 0.000397141
0.054 0.000397141
0.06 0.000397141
0.062 0.000397141
0.066 0.000397141
0.067 0.000397141
0.069 0.000794281
0.088 0.000397141
How would you go about adding a fitting normal distribution to this histogram?