Textbf in Dollar Signs in Tabular (LaTeX)

Question

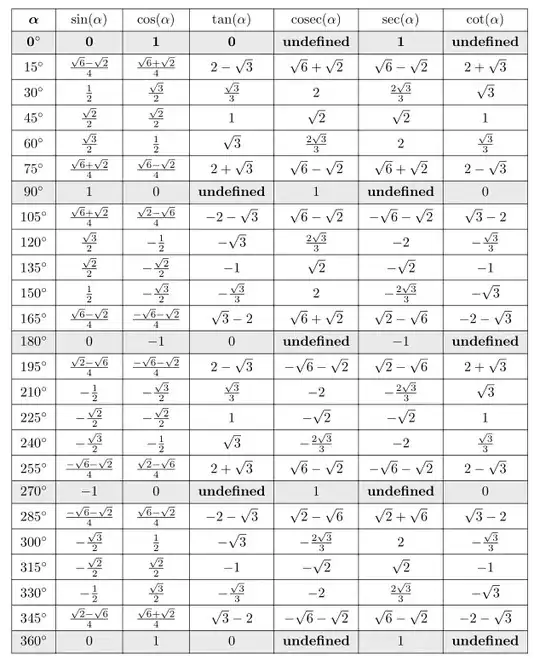
I have been using LaTeX Overleaf (overleaf.com) for some time now, and I have been trying to create a trigonometry table. In the first line of the table, I tried to make the alpha bold in the first cell, but if I put it inside the dollar signs, it would create a lot of errors and crash the pdf converter. If I put the \textbf outside the dollar signs, it would not make the alpha bold. Could anyone please help me fix this problem? Thank you! My code is below this paragraph.

\begin{tabular}{||c|c|c|c||c|c|c||}
\hline
\hline
$\textbf{\alpha}$ &sin($\alpha$) &cos($\alpha$) &tan($\alpha$) &cosec($\alpha$) &sec($\alpha$) &cot($\alpha$)\\
\hline
\hline
\textbf{0}$^\circ$ & $\textbf{0}$ &$\textbf{1}$ &$\textbf{0}$ &\textbf{undefined} &$\textbf{1}$ &\textbf{undefined}\\
\hline
\hline
$15^\circ$ &$\frac{\sqrt{6}-\sqrt{2}}{4}$ &$\frac{\sqrt{6}+\sqrt{2}}{4}$ &$2-\sqrt{3}$ &$\sqrt{6}+\sqrt{2}$ &$\sqrt{6}-\sqrt{2}$ &$2+\sqrt{3}$\\
\hline
$30^\circ$ &$\frac{1}{2}$ &$\frac{\sqrt{3}}{2}$ &$\frac{\sqrt{3}}{3}$ &$2$ &$\frac{2\sqrt{3}}{3}$ &$\sqrt{3}$\\
\hline
$45^\circ$ &$\frac{\sqrt{2}}{2}$ &$\frac{\sqrt{2}}{2}$ &$1$ &$\sqrt{2}$ &$\sqrt{2}$ &$1$\\
\hline
$60^\circ$ &$\frac{\sqrt{3}}{2}$ &$\frac{1}{2}$ &$\sqrt{3}$ &$\frac{2\sqrt{3}}{3}$ &$2$ &$\frac{\sqrt{3}}{3}$\\
\hline
$75^\circ$ &$\frac{\sqrt{6}+\sqrt{2}}{4}$ &$\frac{\sqrt{6}-\sqrt{2}}{4}$ &$2+\sqrt{3}$ &$\sqrt{6}-\sqrt{2}$ &$\sqrt{6}+\sqrt{2}$ &$2-\sqrt{3}$\\
\hline
\hline
$90^\circ$ &$1$ &$0$ &undefined &$1$ &undefined &$0$\\
\hline
\hline
$105^\circ$ &$\frac{\sqrt{6}+{\sqrt{2}}}{4}$ &$\frac{\sqrt{2}-\sqrt{6}}{4}$ &$-2-\sqrt{3}$ &$\sqrt{6}-\sqrt{2}$ &$-\sqrt{6}-\sqrt{2}$ &$\sqrt{3}-2$\\
\hline
$120^\circ$ &$\frac{\sqrt{3}}{2}$ &$-\frac{1}{2}$ &$-\sqrt{3}$ &$\frac{2\sqrt{3}}{3}$ &$-2$ &$-\frac{\sqrt{3}}{3}$\\
\hline
$135^\circ$ &$\frac{\sqrt{2}}{2}$ &$-\frac{\sqrt{2}}{2}$ &$-1$ &$\sqrt{2}$ &$-\sqrt{2}$ &$-1$\\
\hline
$150^\circ$ &$\frac{1}{2}$ &$-\frac{\sqrt{3}}{2}$ &$-\frac{\sqrt{3}}{3}$ &$2$ &$-\frac{2\sqrt{3}}{3}$ &$-\sqrt{3}$\\
\hline
$165^\circ$ &$\frac{\sqrt{6}-\sqrt{2}}{4}$ &$\frac{-\sqrt{6}-\sqrt{2}}{4}$ &$\sqrt{3}-2$ &$\sqrt{6}+\sqrt{2}$ &$\sqrt{2}-\sqrt{6}$ &$-2-\sqrt{3}$\\
\hline
\hline
$180^\circ$ &$0$ &$-1$ &$0$ &undefined &$-1$ &undefined\\
\hline
\hline
$195^\circ$ &$\frac{\sqrt{2}-\sqrt{6}}{4}$ &$\frac{-\sqrt{6}-\sqrt{2}}{4}$ &$2-\sqrt{3}$ &$-\sqrt{6}-\sqrt{2}$ &$\sqrt{2}-\sqrt{6}$ &$2+\sqrt{3}$\\
\hline
$210^\circ$ &$-\frac{1}{2}$ &$-\frac{\sqrt{3}}{2}$ &$\frac{\sqrt{3}}{3}$ &$-2$ &$-\frac{2\sqrt{3}}{3}$ &$\sqrt{3}$\\
\hline
$225^\circ$ &$-\frac{\sqrt{2}}{2}$ &$-\frac{\sqrt{2}}{2}$ &$1$ &$-\sqrt{2}$ &$-\sqrt{2}$ &$1$\\
\hline
$240^\circ$ &$-\frac{\sqrt{3}}{2}$ &$-\frac{1}{2}$ &$\sqrt{3}$ &$-\frac{2\sqrt{3}}{3}$ &$-2$ &$\frac{\sqrt{3}}{3}$\\
\hline
$255^\circ$ &$\frac{-\sqrt{6}-\sqrt{2}}{4}$ &$\frac{\sqrt{2}-\sqrt{6}}{4}$ &$2+\sqrt{3}$ &$\sqrt{6}-\sqrt{2}$ &$-\sqrt{6}-\sqrt{2}$ &$2-\sqrt{3}$\\
\hline
\hline
$270^\circ$ &$-1$ &$0$ &undefined &$1$ &undefined &$0$\\
\hline
\hline
$285^\circ$ &$\frac{-\sqrt{6}-\sqrt{2}}{4}$ &$\frac{\sqrt{6}-\sqrt{2}}{4}$ &$-2-\sqrt{3}$ &$\sqrt{2}-\sqrt{6}$ &$\sqrt{2}+\sqrt{6}$ &$\sqrt{3}-2$\\
\hline
$300^\circ$ &$-\frac{\sqrt{3}}{2}$ &$\frac{1}{2}$ &$-\sqrt{3}$ &$-\frac{2\sqrt{3}}{3}$ &$2$ &$-\frac{\sqrt{3}}{3}$\\
\hline
$315^\circ$ &$-\frac{\sqrt{2}}{2}$ &$\frac{\sqrt{2}}{2}$ &$-1$ &$-\sqrt{2}$ &$\sqrt{2}$ &$-1$\\
\hline
$330^\circ$ &$-\frac{1}{2}$ &$\frac{\sqrt{3}}{2}$ &$-\frac{\sqrt{3}}{3}$ &$-2$ &$\frac{2\sqrt{3}}{3}$ &$-\sqrt{3}$\\
\hline
$345^\circ$ &$\frac{\sqrt{2}-\sqrt{6}}{4}$ &$\frac{\sqrt{6}+\sqrt{2}}{4}$ &$\sqrt{3}-2$ &$-\sqrt{6}-\sqrt{2}$ &$\sqrt{6}-\sqrt{2}$ &$-2-\sqrt{3}$\\
\hline
\hline
$360^\circ$ &$0$ &$1$ &$0$ &undefined &$1$ &undefined\\
\hline
\hline
\end{tabular}
\end{center}

Welcome to TeX.SE!. Load \amsmath in preamble and than for bold \alpha use: $\boldsymbol{\alpha}$ — Zarko, Apr 17 '22 at 08:09
\textbf argumen is for text, you can no use math commands such as \alpha — David Carlisle, Apr 17 '22 at 08:13
Unrelated: usually for floats you should use \centering instead of \begin{center} ... \end{center}. See https://tex.stackexchange.com/q/2651/219947 — Imran, Apr 17 '22 at 08:28

score 2 · Accepted Answer · answered Apr 17 '22 at 08:36

You may liked the following table design:

By put table in display math environment and use tabularray package the table code is much shorter and table become much nicer. Of course, instead of textbf{<text>} and \textbf{<symbol>} you should use mathbf{<text>} and \boldsymbol{<symbol>} respectively

\documentclass{article}
\usepackage{xcolor}
\usepackage{tabularray}
\UseTblrLibrary{amsmath}
\DeclareMathOperator{\cosec}{cosec}
\begin{document}
    [
\begin{tblr}{hlines, vlines,
             cells = {c},
             row{2,8,14,20,Z} = {bg=gray!20}
             }
\boldsymbol{\alpha} & \sin(\alpha) & \cos(\alpha) & \tan(\alpha)  &\cosec(\alpha) & \sec(\alpha) & \cot(\alpha) \
%
\mathbf{0}^\circ & \mathbf{0} &\mathbf{1} &\mathbf{0} &\mathbf{undefined} &\mathbf{1} &\mathbf{undefined}\
15^\circ &\frac{\sqrt{6}-\sqrt{2}}{4} &\frac{\sqrt{6}+\sqrt{2}}{4} &2-\sqrt{3} &\sqrt{6}+\sqrt{2} &\sqrt{6}-\sqrt{2} &2+\sqrt{3}\
30^\circ &\frac{1}{2} &\frac{\sqrt{3}}{2} &\frac{\sqrt{3}}{3} &2 &\frac{2\sqrt{3}}{3} &\sqrt{3}\
45^\circ &\frac{\sqrt{2}}{2} &\frac{\sqrt{2}}{2} &1 &\sqrt{2} &\sqrt{2} &1\
60^\circ &\frac{\sqrt{3}}{2} &\frac{1}{2} &\sqrt{3} &\frac{2\sqrt{3}}{3} &2 &\frac{\sqrt{3}}{3}\
75^\circ &\frac{\sqrt{6}+\sqrt{2}}{4} &\frac{\sqrt{6}-\sqrt{2}}{4} &2+\sqrt{3} &\sqrt{6}-\sqrt{2} &\sqrt{6}+\sqrt{2} &2-\sqrt{3}\
90^\circ &1 &0 &\mathbf{undefined} &1 &\mathbf{undefined} &0\
105^\circ &\frac{\sqrt{6}+{\sqrt{2}}}{4} &\frac{\sqrt{2}-\sqrt{6}}{4} &-2-\sqrt{3} &\sqrt{6}-\sqrt{2} &-\sqrt{6}-\sqrt{2} &\sqrt{3}-2\
120^\circ &\frac{\sqrt{3}}{2} &-\frac{1}{2} &-\sqrt{3} &\frac{2\sqrt{3}}{3} &-2 &-\frac{\sqrt{3}}{3}\
135^\circ &\frac{\sqrt{2}}{2} &-\frac{\sqrt{2}}{2} &-1 &\sqrt{2} &-\sqrt{2} &-1\
150^\circ &\frac{1}{2} &-\frac{\sqrt{3}}{2} &-\frac{\sqrt{3}}{3} &2 &-\frac{2\sqrt{3}}{3} &-\sqrt{3}\
165^\circ &\frac{\sqrt{6}-\sqrt{2}}{4} &\frac{-\sqrt{6}-\sqrt{2}}{4} &\sqrt{3}-2 &\sqrt{6}+\sqrt{2} &\sqrt{2}-\sqrt{6} &-2-\sqrt{3}\
180^\circ &0 &-1 &0 &\mathbf{undefined} &-1 &\mathbf{undefined}\
195^\circ &\frac{\sqrt{2}-\sqrt{6}}{4} &\frac{-\sqrt{6}-\sqrt{2}}{4} &2-\sqrt{3} &-\sqrt{6}-\sqrt{2} &\sqrt{2}-\sqrt{6} &2+\sqrt{3}\
210^\circ &-\frac{1}{2} &-\frac{\sqrt{3}}{2} &\frac{\sqrt{3}}{3} &-2 &-\frac{2\sqrt{3}}{3} &\sqrt{3}\
225^\circ &-\frac{\sqrt{2}}{2} &-\frac{\sqrt{2}}{2} &1 &-\sqrt{2} &-\sqrt{2} &1\
240^\circ &-\frac{\sqrt{3}}{2} &-\frac{1}{2} &\sqrt{3} &-\frac{2\sqrt{3}}{3} &-2 &\frac{\sqrt{3}}{3}\
255^\circ &\frac{-\sqrt{6}-\sqrt{2}}{4} &\frac{\sqrt{2}-\sqrt{6}}{4} &2+\sqrt{3} &\sqrt{6}-\sqrt{2} &-\sqrt{6}-\sqrt{2} &2-\sqrt{3}\
270^\circ &-1 &0 &\mathbf{undefined} &1 &\mathbf{undefined} &0\
285^\circ &\frac{-\sqrt{6}-\sqrt{2}}{4} &\frac{\sqrt{6}-\sqrt{2}}{4} &-2-\sqrt{3} &\sqrt{2}-\sqrt{6} &\sqrt{2}+\sqrt{6} &\sqrt{3}-2\
300^\circ &-\frac{\sqrt{3}}{2} &\frac{1}{2} &-\sqrt{3} &-\frac{2\sqrt{3}}{3} &2 &-\frac{\sqrt{3}}{3}\
315^\circ &-\frac{\sqrt{2}}{2} &\frac{\sqrt{2}}{2} &-1 &-\sqrt{2} &\sqrt{2} &-1\
330^\circ &-\frac{1}{2} &\frac{\sqrt{3}}{2} &-\frac{\sqrt{3}}{3} &-2 &\frac{2\sqrt{3}}{3} &-\sqrt{3}\
345^\circ &\frac{\sqrt{2}-\sqrt{6}}{4} &\frac{\sqrt{6}+\sqrt{2}}{4} &\sqrt{3}-2 &-\sqrt{6}-\sqrt{2} &\sqrt{6}-\sqrt{2} &-2-\sqrt{3}\
360^\circ &0 &1 &0 &\mathbf{undefined} &1 &\mathbf{undefined}\
\end{tblr}
    ]
\end{document}

score 0 · Answer 2 · answered Apr 17 '22 at 08:17

After looking at the comment by Zarko, I know that I can replace $\textbf{\alpha}$ with $\boldsymbol\alpha$ after trying it in my document. The code that works here is:

\begin{tabular}{||c|c|c|c||c|c|c||}
\hline
\hline
$\boldsymbol\alpha$ &sin($\alpha$) &cos($\alpha$) &tan($\alpha$) &cosec($\alpha$) &sec($\alpha$) &cot($\alpha$)\\
\hline
\hline
\textbf{0}$^\circ$ & $\textbf{0}$ &$\textbf{1}$ &$\textbf{0}$ &\textbf{undefined} &$\textbf{1}$ &\textbf{undefined}\\
\hline
\hline
$15^\circ$ &$\frac{\sqrt{6}-\sqrt{2}}{4}$ &$\frac{\sqrt{6}+\sqrt{2}}{4}$ &$2-\sqrt{3}$ &$\sqrt{6}+\sqrt{2}$ &$\sqrt{6}-\sqrt{2}$ &$2+\sqrt{3}$\\
\hline
$30^\circ$ &$\frac{1}{2}$ &$\frac{\sqrt{3}}{2}$ &$\frac{\sqrt{3}}{3}$ &$2$ &$\frac{2\sqrt{3}}{3}$ &$\sqrt{3}$\\
\hline
$45^\circ$ &$\frac{\sqrt{2}}{2}$ &$\frac{\sqrt{2}}{2}$ &$1$ &$\sqrt{2}$ &$\sqrt{2}$ &$1$\\
\hline
$60^\circ$ &$\frac{\sqrt{3}}{2}$ &$\frac{1}{2}$ &$\sqrt{3}$ &$\frac{2\sqrt{3}}{3}$ &$2$ &$\frac{\sqrt{3}}{3}$\\
\hline
$75^\circ$ &$\frac{\sqrt{6}+\sqrt{2}}{4}$ &$\frac{\sqrt{6}-\sqrt{2}}{4}$ &$2+\sqrt{3}$ &$\sqrt{6}-\sqrt{2}$ &$\sqrt{6}+\sqrt{2}$ &$2-\sqrt{3}$\\
\hline
\hline
$90^\circ$ &$1$ &$0$ &undefined &$1$ &undefined &$0$\\
\hline
\hline
$105^\circ$ &$\frac{\sqrt{6}+{\sqrt{2}}}{4}$ &$\frac{\sqrt{2}-\sqrt{6}}{4}$ &$-2-\sqrt{3}$ &$\sqrt{6}-\sqrt{2}$ &$-\sqrt{6}-\sqrt{2}$ &$\sqrt{3}-2$\\
\hline
$120^\circ$ &$\frac{\sqrt{3}}{2}$ &$-\frac{1}{2}$ &$-\sqrt{3}$ &$\frac{2\sqrt{3}}{3}$ &$-2$ &$-\frac{\sqrt{3}}{3}$\\
\hline
$135^\circ$ &$\frac{\sqrt{2}}{2}$ &$-\frac{\sqrt{2}}{2}$ &$-1$ &$\sqrt{2}$ &$-\sqrt{2}$ &$-1$\\
\hline
$150^\circ$ &$\frac{1}{2}$ &$-\frac{\sqrt{3}}{2}$ &$-\frac{\sqrt{3}}{3}$ &$2$ &$-\frac{2\sqrt{3}}{3}$ &$-\sqrt{3}$\\
\hline
$165^\circ$ &$\frac{\sqrt{6}-\sqrt{2}}{4}$ &$\frac{-\sqrt{6}-\sqrt{2}}{4}$ &$\sqrt{3}-2$ &$\sqrt{6}+\sqrt{2}$ &$\sqrt{2}-\sqrt{6}$ &$-2-\sqrt{3}$\\
\hline
\hline
$180^\circ$ &$0$ &$-1$ &$0$ &undefined &$-1$ &undefined\\
\hline
\hline
$195^\circ$ &$\frac{\sqrt{2}-\sqrt{6}}{4}$ &$\frac{-\sqrt{6}-\sqrt{2}}{4}$ &$2-\sqrt{3}$ &$-\sqrt{6}-\sqrt{2}$ &$\sqrt{2}-\sqrt{6}$ &$2+\sqrt{3}$\\
\hline
$210^\circ$ &$-\frac{1}{2}$ &$-\frac{\sqrt{3}}{2}$ &$\frac{\sqrt{3}}{3}$ &$-2$ &$-\frac{2\sqrt{3}}{3}$ &$\sqrt{3}$\\
\hline
$225^\circ$ &$-\frac{\sqrt{2}}{2}$ &$-\frac{\sqrt{2}}{2}$ &$1$ &$-\sqrt{2}$ &$-\sqrt{2}$ &$1$\\
\hline
$240^\circ$ &$-\frac{\sqrt{3}}{2}$ &$-\frac{1}{2}$ &$\sqrt{3}$ &$-\frac{2\sqrt{3}}{3}$ &$-2$ &$\frac{\sqrt{3}}{3}$\\
\hline
$255^\circ$ &$\frac{-\sqrt{6}-\sqrt{2}}{4}$ &$\frac{\sqrt{2}-\sqrt{6}}{4}$ &$2+\sqrt{3}$ &$\sqrt{6}-\sqrt{2}$ &$-\sqrt{6}-\sqrt{2}$ &$2-\sqrt{3}$\\
\hline
\hline
$270^\circ$ &$-1$ &$0$ &undefined &$1$ &undefined &$0$\\
\hline
\hline
$285^\circ$ &$\frac{-\sqrt{6}-\sqrt{2}}{4}$ &$\frac{\sqrt{6}-\sqrt{2}}{4}$ &$-2-\sqrt{3}$ &$\sqrt{2}-\sqrt{6}$ &$\sqrt{2}+\sqrt{6}$ &$\sqrt{3}-2$\\
\hline
$300^\circ$ &$-\frac{\sqrt{3}}{2}$ &$\frac{1}{2}$ &$-\sqrt{3}$ &$-\frac{2\sqrt{3}}{3}$ &$2$ &$-\frac{\sqrt{3}}{3}$\\
\hline
$315^\circ$ &$-\frac{\sqrt{2}}{2}$ &$\frac{\sqrt{2}}{2}$ &$-1$ &$-\sqrt{2}$ &$\sqrt{2}$ &$-1$\\
\hline
$330^\circ$ &$-\frac{1}{2}$ &$\frac{\sqrt{3}}{2}$ &$-\frac{\sqrt{3}}{3}$ &$-2$ &$\frac{2\sqrt{3}}{3}$ &$-\sqrt{3}$\\
\hline
$345^\circ$ &$\frac{\sqrt{2}-\sqrt{6}}{4}$ &$\frac{\sqrt{6}+\sqrt{2}}{4}$ &$\sqrt{3}-2$ &$-\sqrt{6}-\sqrt{2}$ &$\sqrt{6}-\sqrt{2}$ &$-2-\sqrt{3}$\\
\hline
\hline
$360^\circ$ &$0$ &$1$ &$0$ &undefined &$1$ &undefined\\
\hline
\hline
\end{tabular}
\end{center}

Textbf in Dollar Signs in Tabular (LaTeX)

2 Answers2