9

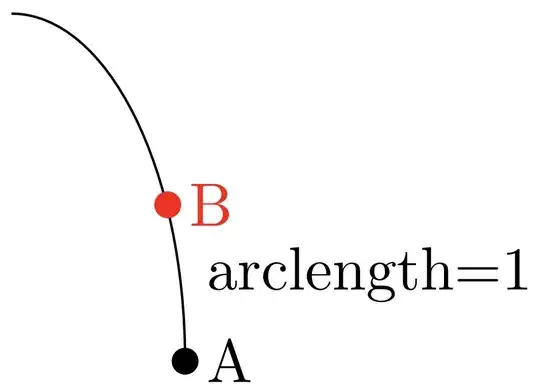
Consider following example:

\documentclass{report}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
\draw (0,0) arc (0:90:1 and 2);
\filldraw (0,0) circle (2pt);
\filldraw[red] (-.1,.9) circle (2pt);
\end{tikzpicture}
\end{document}

enter image description here

Given a curve and an origin (A in the example), I would like to place a point on the curve at a given arclength from the origin (B at an arclength 1 in the example).

How can I achieve this? I found this question and this question, but do not see how to specify the arclength.

Karlo
  • 3,257

1 Answers1

10

This can be done (approximately) with decorations.markings, which accepts lengths (as well as percentages) for its position.

enter image description here

All markings in the image are at 1cm.

Define a style arclen that takes a length as its argument. Then \draw[arclen=1cm] <path> will make the mark at 1cm from the start.

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary {decorations.markings}

\tikzset{arclen/.style={decoration={markings, mark=at position #1 with{\filldraw[red] (0,0) circle (2pt);}},
    postaction=decorate}}


\begin{document}
\begin{tikzpicture}
\drawgray!50, very thin grid (-2,2);
\draw[arclen=1cm] (0,0) -- (0,2);
\draw[arclen=1cm] (0,0) arc (0:90:1 and 2);
\draw[arclen=1cm] (0,0) arc (0:180:1);
\draw[arclen=1cm] (0,0) arc (0:270:.5);
\draw[arclen=1cm] (0,0) arc (0:330:.4);
\draw[arclen=1cm] (0,0) arc (0:330:.3);
\end{tikzpicture}
\end{document}
Sandy G
  • 42,558
  • +1. Really interesting, especially if we know that the length may be defined by an integral not expressed by elementary functions. – Przemysław Scherwentke May 21 '22 at 01:31
  • 3
    @PrzemysławScherwentke the “curve” is really a sequence of line segments. So there’s no integral involved. Just a sum. I suspect that if you tried this on a segment with large curvature you would see some inaccuracies. But I haven’t looked at the raw code to see how tikz calculates the number of points. – Sandy G May 21 '22 at 02:16
  • This is so nice, I didn't know it, thanks Sandy. +1 – SebGlav May 21 '22 at 07:46
  • 1
    @SebGlav: Glad I could show you something new for a change. It's usually the other way around. – Sandy G May 21 '22 at 14:57