I was trying to edit this answer a bit, I wanted to put 5 or 6 arrows on the red and blue lines, I couldn't do it. The only thing I managed to do is this: (a lot of arrows come out and it's not what I want) any ideas how to fix this?
I have also tried to make the red and blue lines respect the sphere, that is to say that it is more transparent when the graph is passing behind the sphere and it is normal when it is in front, but I have not achieved anything.
\documentclass{standalone}
\usepackage{pst-ode,pst-3dplot}
\begin{document}
\begin{pspicture}(-1.1,-1.1)(1.1,1.1)%
% Sphere
\pstThreeDSpherelinewidth=0.0001pt,strokeopacity=0.3,linecolor=gray,SegmentColor={[cmyk]{0.0,0.0,0.0,0.2}}{1}
% lower half-space
\pstODEsolve[algebraic]{XYZa}{0 1 2}{0}{35}{500}{1e-9 0.0 -1.0}{
-x[1]+x[0]x[2]^2 |
x[0]+x[1]x[2]^2 |
-x[2]*(x[0]^2+x[1]^2)
}
\psset{arrowscale=0.4}
\listplotThreeD[linecolor=blue,linewidth=0.3pt,ArrowInside=->,ArrowInsidePos=1]{XYZa}
% upper half-space
\pstODEsolve[algebraic]{XYZb}{0 1 2}{0}{35}{500}{1e-9 0.0 1.0}{
-x[1]+x[0]x[2]^2 |
x[0]+x[1]x[2]^2 |
-x[2]*(x[0]^2+x[1]^2)
}
\listplotThreeD[linecolor=red,linewidth=0.4pt,ArrowInside=->,ArrowInsidePos=1]{XYZb}
\end{pspicture}
\end{document}
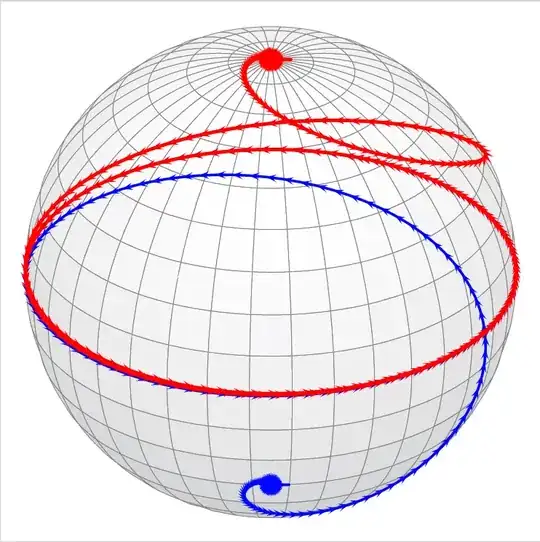
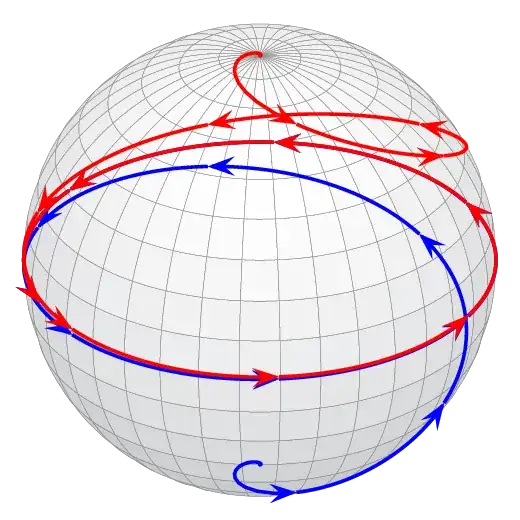
tikz-pgfandgraphicstags for? – Dr. Manuel Kuehner May 23 '22 at 01:14tikz-pgffor example, so I drew your attention by tagging them. It was just that. – Zaragosa May 23 '22 at 01:31