One possible solution:
- wider
\textwidth determined by use of the geometry package
footnotesize font size- different widths of columns
- use of the
tabularray package
\documentclass{article}
\usepackage{geometry}
\usepackage{microtype}
\usepackage{tabularray}
\begin{document}
\begin{center}
\footnotesize
\begin{tblr}{hlines, vlines,
colspec = {c X[0.5, c] X[2.2, j] *{4}{X[0.7, c]}},
colsep = 3pt,
row{1,2} = {font=\bfseries, c, m}
}
\SetCell[c=7]{c} Data Structures
& & & & & & \
No & Sigma name and all
& Idea & Construct Time (Runtime Time)
& Construct Time (Space)
& Searching data (Query)
& Search head (Space) \
1 & ABCD & These algorithms achieve performance better than the classic
& O(NLkt)
& O(nL) & O(L(kt + dnp)
& O(1) \
2 & FGH & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces
& $O(dn \log n)$
& $O(dn)$
& 222 & $O(1)$ \
3 & LMPQ & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces
& 008 & 666 & 242 & 333 \
4 & RSTV & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces
& 012 & 888 & 333 & 55 \
5 & ZMNQ & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces
& 016 & 888 & 444 & 343 \
6 & WORP & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces and MBR
& 020 & 555 & 444 & 333 \
7 & MNPO & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces. Search based on data pruning and the radius of nodes.
& 024 & 888 & 224 & 342 \
\end{tblr}
\end{center}
\end{document}
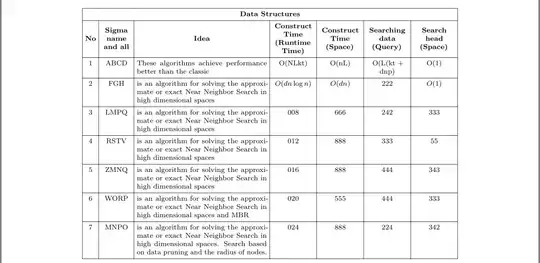
(grey lines are page borders)
Addendum:
Yes, this table can be set on classical way, which can be compiled also on Overleaf. Code as well result are lef elegant, but solution works:
\documentclass{article}
\usepackage{geometry}
\usepackage{microtype}
\usepackage{ragged2e}
\usepackage{tabularx}
\newcolumntype{C}[1]{>{\hsize=#1\hsize\linewidth=\hsize%
\Centering}X}
\newcolumntype{L}[1]{>{\hsize=#1\hsize\linewidth=\hsize%
\RaggedRight\hspace{0pt}}X}
\begin{document}
\begin{center}
\footnotesize
\setlength\tabcolsep{3pt}
\begin{tabularx}{\textwidth}{|c | C{0.7} | L{2.5} | *{4}{C{0.7}|} }
%
\hline
\multicolumn{7}{|c|}{\textbf{Data Structures}} \
\hline
\textbf{No}
& \textbf{Sigma name and all}
& \centering\textbf{Idea}
& \textbf{Construct Time (Runtime Time)}
& \textbf{Construct Time (Space)}
& \textbf{Searching data (Query)}
& \textbf{Search head (Space)}
\
\hline
1 & ABCD & These algorithms achieve performance better than the classic
& O(NLkt)
& O(nL) & O(L(kt + dnp)
& O(1) \
\hline
2 & FGH & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces
& $O(dn \log n)$
& $O(dn)$
& 222 & $O(1)$ \
\hline
3 & LMPQ & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces
& 008 & 666 & 242 & 333 \
\hline
4 & RSTV & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces
& 012 & 888 & 333 & 55 \
\hline
5 & ZMNQ & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces
& 016 & 888 & 444 & 343 \
\hline
6 & WORP & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces and MBR
& 020 & 555 & 444 & 333 \
\hline
7 & MNPO & is an algorithm for solving the approximate or exact Near Neighbor Search in high dimensional spaces. Search based on data pruning and the radius of nodes.
& 024 & 888 & 224 & 342 \
\hline
\end{tabularx}
\end{center}
\end{document}
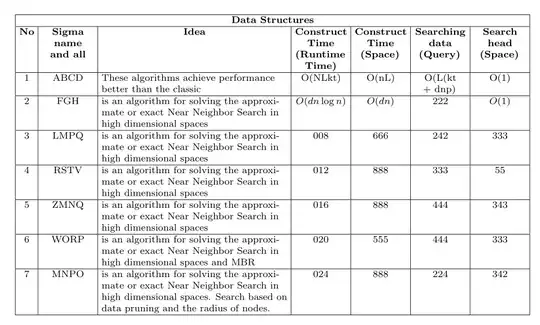


landscape, minimal allowed font size, can column headers be shortened, etc. – Zarko May 26 '22 at 06:16