0

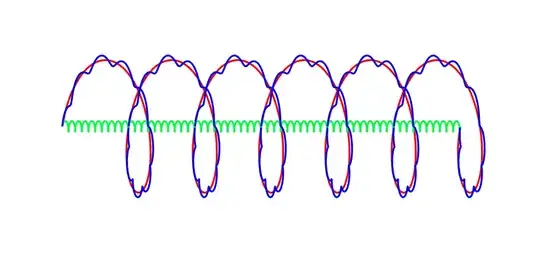
I have two coils, which I make with code from here

I want to add the coils together, like cos(x) + cos(2x), to get a new one. But I am not sure this is even possible with how I made them. Can it be done?

If it can't be done, I would appreciate any help in drawing helices using mathematical functions -- it would then be trivial to add them. I tried this first but couldn't figure it out.

The code is:

\documentclass[11pt]{article}

\usepackage{tikz}
\usetikzlibrary{decorations.markings}
\usetikzlibrary{calc,intersections,through}
\usetikzlibrary{bending}
\usetikzlibrary{shapes.geometric}
\tikzset{point/.style={circle,inner sep=0pt,minimum size=3pt,fill=black}}


\usetikzlibrary{arrows}


\usetikzlibrary{decorations.pathmorphing}


\makeatletter


% gluon decoration (based on the original coil decoration)


\pgfdeclaredecoration{gluon}{coil}
{
  \state{coil}[switch if less than=%
    0.5\pgfdecorationsegmentlength+%>
    \pgfdecorationsegmentaspect\pgfdecorationsegmentamplitude+%
    \pgfdecorationsegmentaspect\pgfdecorationsegmentamplitude to last,
               width=+\pgfdecorationsegmentlength]
  {
    \pgfpathcurveto
    {\pgfpoint@oncoil{0    }{ 0.555}{1}}
    {\pgfpoint@oncoil{0.445}{ 1    }{2}}
    {\pgfpoint@oncoil{1    }{ 1    }{3}}
    \pgfpathcurveto
    {\pgfpoint@oncoil{1.555}{ 1    }{4}}
    {\pgfpoint@oncoil{2    }{ 0.555}{5}}
    {\pgfpoint@oncoil{2    }{ 0    }{6}}
    \pgfpathcurveto
    {\pgfpoint@oncoil{2    }{-0.555}{7}}
    {\pgfpoint@oncoil{1.555}{-1    }{8}}
    {\pgfpoint@oncoil{1    }{-1    }{9}}
    \pgfpathcurveto
    {\pgfpoint@oncoil{0.445}{-1    }{10}}
    {\pgfpoint@oncoil{0    }{-0.555}{11}}
    {\pgfpoint@oncoil{0    }{ 0    }{12}}
  }
  \state{last}[next state=final]
  {
    \pgfpathcurveto
    {\pgfpoint@oncoil{0    }{ 0.555}{1}}
    {\pgfpoint@oncoil{0.445}{ 1    }{2}}
    {\pgfpoint@oncoil{1    }{ 1    }{3}}
    \pgfpathcurveto
    {\pgfpoint@oncoil{1.555}{ 1    }{4}}
    {\pgfpoint@oncoil{2    }{ 0.555}{5}}
    {\pgfpoint@oncoil{2    }{ 0    }{6}}
  }
  \state{final}{}
}


\def\pgfpoint@oncoil#1#2#3{%
  \pgf@x=#1\pgfdecorationsegmentamplitude%
  \pgf@x=\pgfdecorationsegmentaspect\pgf@x%
  \pgf@y=#2\pgfdecorationsegmentamplitude%
  \pgf@xa=0.083333333333\pgfdecorationsegmentlength%
  \advance\pgf@x by#3\pgf@xa%
}


\makeatother
\begin{document}


\begin{center}
 \begin{tikzpicture}
    \draw[very thick,rotate=90,decoration={
         aspect=0.41, 
         segment length=.5cm,
         amplitude=.5cm,
         gluon},
     decorate,] (0,10) --(0,0);
 \end{tikzpicture}


\medskip


\begin{tikzpicture}
    \draw[very thick,rotate=90,decoration={
         aspect=0.41, 
         segment length=.25cm,
         amplitude=.25cm,
         gluon},
     decorate,] (0,10) --(0,0);
 \end{tikzpicture}
 \end{center}
\end{document}
Wapiti
  • 407

3 Answers3

1

Like this picture?

enter image description here

The picture has been generated by the code:

\begin{document}

\begin{center}
 \begin{tikzpicture}[scale=.5]
    \draw[very thick,rotate=90,decoration={
         aspect=0.41, 
         segment length=.5cm,
         amplitude=.5cm,
         gluon},
     decorate,] (0,10) --(0,0);
     \filldraw[rotate=90] (0,10) circle(5pt);
     \draw[very thick,rotate=90,decoration={
        aspect=0.41, 
        segment length=.25cm,
        amplitude=.25cm,
        gluon},
     decorate,] (0,20)--(0,10);
     \medskip
 \end{tikzpicture}


\end{center}
\end{document}

where the preambule come from your code.

Raffaele Santoro
  • 9,702
1

You can eliminate the need to customize your own coil by the usage of shorten >= <some value>.

Output

\documentclass[margin=3.14mm]{standalone}
\usepackage{tikz}
\usetikzlibrary{decorations.pathmorphing}

\begin{document}
\begin{tikzpicture}[
    pics/mycoil/.style={
        code={
        % larger coil
         \draw[
            very thick, 
            decoration={
                coil, aspect=0.41, segment length=0.5cm, amplitude=0.5cm
            },
            decorate, shorten >=9pt
        ] (0, 0) -- (1.5, 0);
        % smaller coil
        \draw[
            very thick, 
            decoration={
                coil, aspect=0.41, segment length=0.25cm, amplitude=0.25cm
            },
            decorate,  shorten >=4.25pt, xshift=-9.5pt
        ] (1.5,0) -- (2.5,0);
    },
}
]
\pic foreach \x in {1,...,5} at (2*\x,0) {mycoil};


% extra for explanation purposes
\draw[very thick,
    decoration={coil, aspect=0.41, segment length=0.25cm, amplitude=0.25cm}, decorate
] (2, -1) --
node[pos=1, right]{\small Remove horizontal line at the end by using \texttt{shorten >= value}}
(3, -1);
\draw node[draw=red, thick, circle, minimum size=4pt, xshift=-3pt] at (3, -1) {};
\end{tikzpicture}
\end{document}
M. Al Jumaily
  • 4,035
  • 2
  • 11
  • 26
  • Okay but isn't this just splicing together and alternating two different helices? I need to add them together like cos(x) + cos(2x). – Wapiti Jun 15 '22 at 18:12
  • Removing the horizontal line is great though, thanks for that. – Wapiti Jun 15 '22 at 18:13
1
\documentclass[tikz, border=1cm]{standalone}
\begin{document}
\begin{tikzpicture}

\draw[red, domain=0:1, smooth, variable=\t] (0,0) \foreach \n in {0,...,5} {-- plot ( {0.5*(\t+\n)-0.2*cos(\t*2*pi r)+0.2} , {0.5*sin(\t*2*pi r)})};

\draw[green, domain=0:1, smooth, variable=\t, samples=100]  (0,0) \foreach \n in {0,...,5} {-- plot ( {0.5*(\t+\n)-0.01*cos(\t*20*pi r)+0.01} , {0.04*sin(\t*20*pi r)})};

\draw[blue, domain=0:1, smooth, variable=\t, samples=100] (0,0) \foreach \n in {0,...,5} {-- plot ( {0.5*(\t+\n)-0.2*cos(\t*2*pi r)+0.2-0.01*cos(\t*20*pi r)+0.01} , {0.5*sin(\t*2*pi r)+0.04*sin(\t*20*pi r)})};

\end{tikzpicture}
\end{document}

Two coils and their "sum"

hpekristiansen
  • 37,006
  • Yes, this is much better. I need to learn this coding language rather than hacking together random things. – Wapiti Jun 15 '22 at 15:22
  • @Wapiti It's just tikz / pgfplots, but since searching around the site you'll inevitably find tex solutions you might want to learn tex as well. – user202729 Jun 15 '22 at 15:46
  • @user202729: Surely you mean LaTeX!? Only very few people use TeX nowadays. – hpekristiansen Jun 15 '22 at 15:50
  • As in learn it as a programming language. You need to know tex anyway. – user202729 Jun 15 '22 at 15:56
  • I know LaTeX, but tikz and pfgplots coding I have not yet really figured out. Unfortunately the solution you have offered @hpekristiansen is not general. It is not actually using a helical equation as I originally thought, so trying to alter the parameters to increase radius, for example, results in a big mess. Also there are small gaps between the pieces. Perhaps if there were not magic constants doing the work this solution would be generalizable? I would be happy to accept this answer if you can help me understand what the scalars are doing and how to generalize. – Wapiti Jun 15 '22 at 18:11
  • I see no simple way to avoid the gaps - it can probably be done with spath3, as there is a limit on how large an angle you can use in cos or sin. The coil is just an ellipse that moves. I have chosen the the parameter \t to be the fraction of a turn in the ellipse. The constants are amplitudes and pitch of movement. @Wapiti: You have not really explained what you mean by "add the coils together" other than "like cos(x) + cos(2x)" - and this is exactly what I do in this answer. – hpekristiansen Jun 15 '22 at 18:21
  • 1
    I just remembered that the foreach can be moved inside the \draw - this removes the gaps. – hpekristiansen Jun 15 '22 at 20:16
  • OK this is the best answer by far as it actually spells out how to do what I asked. Thanks. – Wapiti Jun 18 '22 at 12:56