\documentclass[oneside,DIV=12]{scrbook}
\usepackage{scrhack}
\usepackage{mathtools, amsthm, amssymb}
\usepackage[warnings-off={mathtools-colon,mathtools-overbracket}]{unicode-math}
\setmathfont{Latin Modern Math}
\usepackage{xparse}
\usepackage{xpatch}
\usepackage{xstring}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% \ExpandArg (https://tex.stackexchange.com/a/515425)
\ExplSyntaxOn
\cs_new_protected:Nn __user_expand_arg:n
{
\tl_set:No \ProcessedArgument { #1 }
}
\cs_set_eq:NN \ExpandArg __user_expand_arg:n
\ExplSyntaxOff
% \ZapSpaces (https://tex.stackexchange.com/a/652826)
\ExplSyntaxOn
\cs_new_protected:Npn __user_arg_zap_spaces:n #1
{
\tl_set:Nn \ProcessedArgument {#1}
\tl_remove_all:Nn \ProcessedArgument { ~ }
}
\cs_set_eq:NN \ZapSpaces __user_arg_zap_spaces:n
\ExplSyntaxOff
% \polycoeff{<polynomial>} and \coeff (n < 10) (https://tex.stackexchange.com/a/649027)
\newcount\coefnum
\newcount\expnum
\def\polycoeff#1{\polyA#1\relax}
\def\polyA{\afterassignment\polyB \coefnum=}
\def\polyB#1{\ifx#1\relax \sxdef{polyco:0}{\the\coefnum}%
\else \expandafter\polyC \fi
}
\def\polyC#1{\afterassignment\polyD \expnum=\ifx^#1\else 1 #1\fi}
\def\polyD{\sxdef{polyco:\the\expnum}{\the\coefnum}\polyA}
\def\coeff#1{\ifcsname polyco:#1\endcsname \csname polyco:#1\endcsname
\else 0\fi
}
\def\sxdef#1{\expandafter\xdef\csname#1\endcsname}
% \PolyCoeff(<polynomial>), \Coeff (n < 10), and \Coefficients
\newcommand{\Polynomial}{}
\NewDocumentCommand{\PolyCoeff}{>{\ZapSpaces} >{\ExpandArg} m}{%
\renewcommand{\Polynomial}{+#1.}
% x^5
\IfSubStr{\Polynomial}{++x^5}{\xpatchcmd{\Polynomial}{++x^5}{1x^5}{}{}}{}
\IfSubStr{\Polynomial}{+x^5}{\xpatchcmd{\Polynomial}{+x^5}{1x^5}{}{}}{}
\IfSubStr{\Polynomial}{+-x^5}{\xpatchcmd{\Polynomial}{+-x^5}{-1x^5}{}{}}{}
\IfSubStr{\Polynomial}{-x^5}{\xpatchcmd{\Polynomial}{-x^5}{-1x^5}{}{}}{}
\IfSubStr{\Polynomial}{x^5.}{\xpatchcmd{\Polynomial}{x^5.}{1x^5+0}{}{}}{}
% x^4
\IfSubStr{\Polynomial}{++x^4}{\xpatchcmd{\Polynomial}{++x^4}{1x^4}{}{}}{}
\IfSubStr{\Polynomial}{+x^4}{\xpatchcmd{\Polynomial}{+x^4}{+1x^4}{}{}}{}
\IfSubStr{\Polynomial}{+-x^4}{\xpatchcmd{\Polynomial}{+-x^4}{-1x^4}{}{}}{}
\IfSubStr{\Polynomial}{-x^4}{\xpatchcmd{\Polynomial}{-x^4}{-1x^4}{}{}}{}
\IfSubStr{\Polynomial}{x^4.}{\xpatchcmd{\Polynomial}{x^4.}{1x^4+0}{}{}}{}
% x^3
\IfSubStr{\Polynomial}{++x^3}{\xpatchcmd{\Polynomial}{++x^3}{1x^3}{}{}}{}
\IfSubStr{\Polynomial}{+x^3}{\xpatchcmd{\Polynomial}{+x^3}{+1x^3}{}{}}{}
\IfSubStr{\Polynomial}{+-x^3}{\xpatchcmd{\Polynomial}{+-x^3}{-1x^3}{}{}}{}
\IfSubStr{\Polynomial}{-x^3}{\xpatchcmd{\Polynomial}{-x^3}{-1x^3}{}{}}{}
\IfSubStr{\Polynomial}{x^3.}{\xpatchcmd{\Polynomial}{x^3.}{1x^3+0}{}{}}{}
% x^2
\IfSubStr{\Polynomial}{++x^2}{\xpatchcmd{\Polynomial}{++x^2}{1x^2}{}{}}{}
\IfSubStr{\Polynomial}{+x^2}{\xpatchcmd{\Polynomial}{+x^2}{+1x^2}{}{}}{}
\IfSubStr{\Polynomial}{+-x^2}{\xpatchcmd{\Polynomial}{+-x^2}{-1x^2}{}{}}{}
\IfSubStr{\Polynomial}{-x^2}{\xpatchcmd{\Polynomial}{-x^2}{-1x^2}{}{}}{}
\IfSubStr{\Polynomial}{x^2.}{\xpatchcmd{\Polynomial}{x^2.}{1x^2+0}{}{}}{}
% x^1
\IfSubStr{\Polynomial}{++x+}{\xpatchcmd{\Polynomial}{++x+}{1x+}{}{}}{}
\IfSubStr{\Polynomial}{++x-}{\xpatchcmd{\Polynomial}{++x-}{1x-}{}{}}{}
\IfSubStr{\Polynomial}{++x.}{\xpatchcmd{\Polynomial}{++x.}{1x+0}{}{}}{}
\IfSubStr{\Polynomial}{+x+}{\xpatchcmd{\Polynomial}{+x+}{+1x+}{}{}}{}
\IfSubStr{\Polynomial}{+x-}{\xpatchcmd{\Polynomial}{+x-}{+1x-}{}{}}{}
\IfSubStr{\Polynomial}{+x.}{\xpatchcmd{\Polynomial}{+x.}{+1x+0}{}{}}{}
\IfSubStr{\Polynomial}{-x+}{\xpatchcmd{\Polynomial}{-x+}{-1x+}{}{}}{}
\IfSubStr{\Polynomial}{-x-}{\xpatchcmd{\Polynomial}{-x-}{-1x-}{}{}}{}
\IfSubStr{\Polynomial}{-x.}{\xpatchcmd{\Polynomial}{-x.}{-1x+0}{}{}}{}
% x^0
\IfSubStr{\Polynomial}{.}{\xpatchcmd{\Polynomial}{.}{}{}{}}{}
% store coefficients
\polycoeff{\Polynomial}
\renewcommand{\CoeffZero}{\coeff{0}}
\renewcommand{\CoeffOne}{\coeff{1}}
\renewcommand{\CoeffTwo}{\coeff{2}}
\renewcommand{\CoeffThree}{\coeff{3}}
\renewcommand{\CoeffFour}{\coeff{4}}
\renewcommand{\CoeffFive}{\coeff{5}}
}
\newcommand{\CoeffZero}{} % variable corresponding to the coefficient of x^0, i.e., the constant term a_0
\newcommand{\CoeffOne}{} % a_1 of a_1 x
\newcommand{\CoeffTwo}{} % a_2 of a_2 x^2
\newcommand{\CoeffThree}{} % a_3 of a_3 x^3
\newcommand{\CoeffFour}{} % a_4 of a_4 x^4
\newcommand{\CoeffFive}{} % a_5 of a_5 x^5
\newcommand{\Coefficients}{a_5 = \CoeffFive,, a_4 = \CoeffFour,, a_3 = \CoeffThree,, a_2 = \CoeffTwo,, a_1 = \CoeffOne,, a_0 = \CoeffZero.}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\begin{document}\KOMAoptions{DIV=current}\Large%
\newcommand{\quintic}{ 5x^5 - 4x^4 + 3x^3 - 2x^2 + x }
[f(x) = \quintic.]
\PolyCoeff{\quintic}
[\Coefficients]
\end{document}
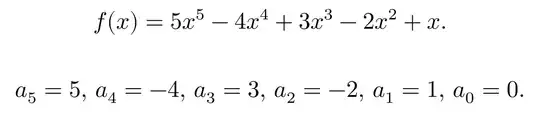
x^nterms, though your description would indicate an input such as the following:\polycoeff{-7+0+5+6}– Skillmon Jun 24 '22 at 18:12\polycoeff{6x^3 + 5x^2 −− 7}or\polycoeff{6x^3 + 5x^2 − − 7}? How to handle\polycoeff{2x^3 + 2x^3 +2x^3 +2x^2+2x^2+x^2 − 7}– Ulrich Diez Jun 27 '22 at 14:25