The formula is:
(1461 * (Y + 4800 + (M - 14)/12))/4 +(367 * (M - 2 - 12 * ((M - 14)/12)))/12 - (3 * ((Y + 4900 + (M - 14)/12)/100))/4 + D - 32075
with the fractional part of the divisions being discarded.
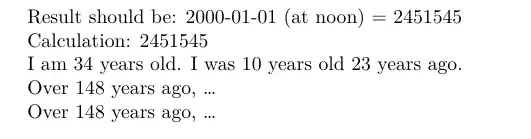
MWE
\documentclass{article}
\usepackage{luacode}
\begin{luacode}
JDN = function(Y, M, D)
-- result = (1461 * (Y + 4800 + (M - 14)/12))/4 +(367 * (M - 2 - 12 * ((M - 14)/12)))/12 - (3 * ((Y + 4900 + (M - 14)/12)/100))/4 + D - 32075
-- tex.sprint("JDN=", result)
-- tex.sprint("\par", math.floor(-2.5),", ",math.modf(-2.5))
-- i,f=math.modf(-2.5)
-- tex.sprint("\par", i)
-- result =
--(1461 * (Y + 4800 + (M - 14)/12))
xa=1461
xb=Y
xc=4800
xd=(M - 14)
xdi,xdf=math.modf(xd/12)
--(1461 * (Y + 4800 + (M - 14)/12))
xe=(xa * (xb + xc + xdi))
xfi,xff=math.modf(xe/4)
--/4
-- + --&&
xg=367
xh= (M - 2 - 12 * xdi)
xji,xjf=math.modf(xg * xh/12)
--(367 * (M - 2 - 12 * ((M - 14)/12)))/12
-- - --&&
xk=3
xl=(Y + 4900 + xdi)
xmi,xmf=math.modf(xk * xl / 100)
--(3 * ((Y + 4900 + (M - 14)/12)/100))
xni,xnf=math.modf(xmi/4)
--/4
-- + --&&
xo = D - 32075
result = xfi + xji - xni + xo
-- tex.sprint("JDN=", result)
return result
end
yeardiff = function(jdn1,jdn2)
resulti,resultf = math.modf((jdn2-jdn1)/365.2425)
return resulti
end
yeardifftoday = function(jdn1)
jdn2=JDN(os.date("%Y"), os.date("%m"), os.date("%d"))
resulti,resultf = math.modf((jdn2-jdn1)/365.2425)
return resulti
end
\end{luacode}
\newcommand\findjdn[3]{%
\directlua{
tex.sprint(JDN(#1, #2, #3))
}}
\newcommand\findyears[6]{%
\directlua{
tex.sprint(yeardiff(JDN(#1, #2, #3), JDN(#4, #5, #6)))
}}
\newcommand\findyearstoday[3]{%
\directlua{
tex.sprint(yeardifftoday(JDN(#1, #2, #3)))
}}
\begin{document}
Result should be:
2000-01-01 (at noon)
= 2451545
Calculation:
\findjdn{2000}{1}{1}
I am
\findyears{1988}{2}{29}{2022}{7}{28}
years
old.
I was
\findyears{1988}{2}{29}{1999}{2}{1}
years old
\findyearstoday{1999}{2}{1}
years ago.
Over
\findyears{1873}{12}{31}{2022}{7}{28}
years ago, \ldots
Over
\findyearstoday{1873}{12}{31}
years ago, \ldots
\end{document}
I've left the working in, so you can double-check if the coding is correct. The lua manual is at: Lua Manual

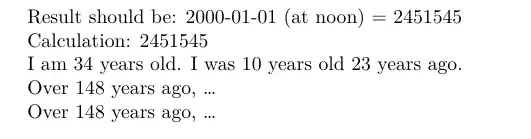
pgfcalendarpackage does that type of calculation, using the formula for Julian day number on Wikipedia. lua script can use the same formula. – Cicada Jul 27 '22 at 15:37