This should work:
\documentclass[12pt]{article}
\usepackage[a4paper,top=0.6 in,bottom=0.6 in,left=0.6 in,right=0.6 in]{geometry}
\usepackage{amsmath}
\begin{document}
\large
\begin{align}
\lambda&=\dfrac{Gr_{x}}{R_{e}^2} & \widetilde{N}&=\dfrac{Gr_{x}^{\ast}}{Gr_{x}} \\[3ex]
Gr_{x}&=\dfrac{g\beta_{T}\left(T_{w}-T_{\infty}\right)x^{3}}{\nu^{2}} & Gr_{x}^{\ast}&=\dfrac{g\beta_{C}\left(C_{w}-C_{\infty}\right)x^{3}}{\nu^{2}}\\[3ex]
M^{2}&=\dfrac{\sigma\,B_{0}^{2}}{a\,\rho\, x^{n-1}} & Nr&=\dfrac{16\sigma^{\ast}}{3k^{\ast}}\,\dfrac{T^{3}_{\infty}}{k_{2}} \\[3ex]
\dfrac{1}{Pr}&=\dfrac{k_{2}}{\rho c_{p}} & A&=\dfrac{b}{a}\\[3ex]
S_{c}&=\dfrac{\nu}{D_{B}} & \dfrac{1}{k_{1}}&=\dfrac{\mu \phi}{k'}\\[3ex]
S_{r}&=\dfrac{D_{m}\,k_{T}\,\left(T_{w}-T_{\infty}\right)}{\alpha_{m}\,C_{p}\,C_{s}\,\left(C_{w}-C_{\infty}\right)} & D_{f}&=\dfrac{D_{m}\,k_{T}\,\left(T_{w}-T_{\infty}\right)}{\alpha_{m}\,C_{p}\,C_{s}\,\left(C_{w}-C_{\infty}\right)}
\end{align}
\end{document}
Removing \begin{equation}, \end{equation} environment and changing align* to align fixes everything.
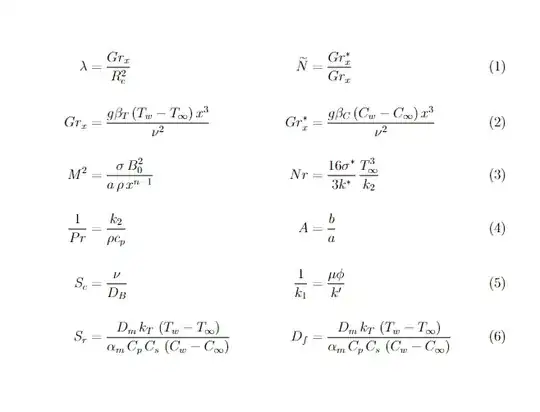
If you want them singularly vertical:
\documentclass[12pt]{article}
\usepackage[a4paper,top=0.6 in,bottom=0.6 in,left=0.6 in,right=0.6 in]{geometry}
\usepackage{amsmath}
\begin{document}
\large
\begin{align}
\lambda=\dfrac{Gr_{x}}{R_{e}^2}
\end{align}
\begin{align}
\widetilde{N}=\dfrac{Gr_{x}^{\ast}}{Gr_{x}}
\end{align}
\begin{align}
Gr_{x}=\dfrac{g\beta_{T}\left(T_{w}-T_{\infty}\right)x^{3}}{\nu^{2}}
\end{align}
\begin{align}
Gr_{x}^{\ast}=\dfrac{g\beta_{C}\left(C_{w}-C_{\infty}\right)x^{3}}{\nu^{2}}
\end{align}
\begin{align}
M^{2}=\dfrac{\sigma,B_{0}^{2}}{a,\rho, x^{n-1}}
\end{align}
\begin{align}
Nr=\dfrac{16\sigma^{\ast}}{3k^{\ast}},\dfrac{T^{3}{\infty}}{k{2}}
\end{align}
\begin{align}
\dfrac{1}{Pr}=\dfrac{k_{2}}{\rho c_{p}}
\end{align}
\begin{align}
A=\dfrac{b}{a}
\end{align}
\begin{align}
S_{c}=\dfrac{\nu}{D_{B}}
\end{align}
\begin{align}
\dfrac{1}{k_{1}}=\dfrac{\mu \phi}{k'}
\end{align}
\begin{align}
S_{r}=\dfrac{D_{m},k_{T},\left(T_{w}-T_{\infty}\right)}{\alpha_{m},C_{p},C_{s},\left(C_{w}-C_{\infty}\right)}
\end{align}
\begin{align}
D_{f}=\dfrac{D_{m},k_{T},\left(T_{w}-T_{\infty}\right)}{\alpha_{m},C_{p},C_{s},\left(C_{w}-C_{\infty}\right)}
\end{align}
\end{document}

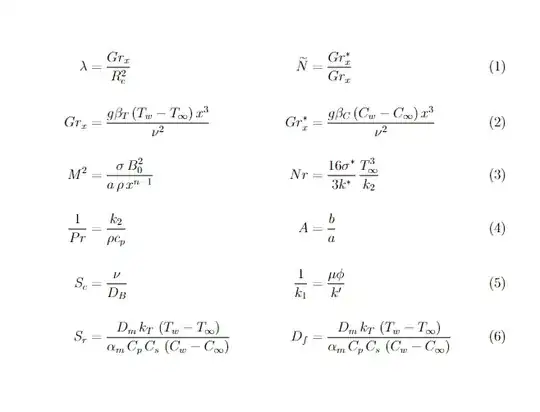

align*insideequation, sincealign*is already a top-level display environment. The error message is pretty clear. Just remove the outerequationenvironment. – campa Aug 17 '22 at 08:56alignedenvironment instead ofalign*within theequationenvironment. – Imran Aug 17 '22 at 11:47