0

I wanted to see some isomorphisms of the Petersen graph; I took the code from here, and run with several layouts from here, but the result with tree layout is not isomorphic to the Petersen graph:

\usetikzlibrary{graphs, graphdrawing, quotes}
\usetikzlibrary{shapes.geometric}
\usetikzlibrary{graphs.standard}
\usegdlibrary{trees, layered}
\usegdlibrary{force,circular,trees}

\begin{document}


\tikz \graph[tree layout, nodes={empty nodes, draw, circle, inner sep=0.45mm, fill=black}, clockwise]
    { subgraph I_n [V={0,1,2,3,4}] --
      subgraph C_n [V={5,6,7,8,9},radius=1.25cm];
      {[cycle] 0,2,4,1,3} };
\end{document}

In this graph built as a Petersen graph there are two points with only two edges

Torbjørn T.
  • 206,688
ocap
  • 3
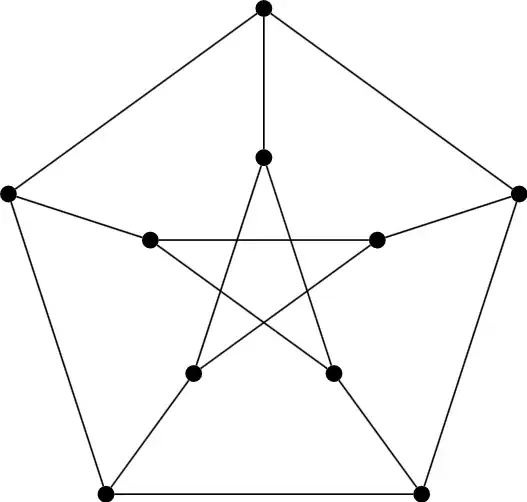
  • If I'm searching the Internet for the phrase Petersen graph I'll see things that do not look like anything I'd classify as a tree layout. – Qrrbrbirlbel Aug 19 '22 at 07:30
  • @Qrrbrbirlbel Right! Thank you! The Petersen graph cannot be planar. The output of the code of a Petersen Graph with "tree layout" is not a Petersen Graph, but it is a Petersen Graph with other layouts. As I wrote in the comment to the answer, probably I failed to understand what layout means here. – ocap Aug 24 '22 at 15:42

1 Answers1

3

I don't think a Petersen graph is considered a graph with a tree layout.

If I remove tree layout from your \graph command I get a very different output.

Code

\documentclass[tikz]{standalone}
\usetikzlibrary{graphs, graphs.standard, graphdrawing}
\usegdlibrary{trees}

\begin{document}
\tikz \graph[
  nodes={empty nodes, draw, fill, circle, inner sep=0.45mm},
  clockwise
] {
  subgraph I_n [V={0,1,2,3,4}]
  --
  subgraph C_n [V={5,6,7,8,9}, radius=1.25cm];
  {[cycle] 0,2,4,1,3};
};
\end{document}

Output

enter image description here

Qrrbrbirlbel
  • 119,821
  • Thank you! My purpose was to find isomorphic graphs to that of Petersen. And my assumption was that changing the layout don't affect the structure of the graph. So, when I ran the code, I thought that either (a) I do not quite understand what a layout is, or (b) There is something wrong in the "tree layout" of tikz-graph. I was inclined to answer (b), because all the other layouts resulted in isomorphic graphs. But by your answer, now I am more inclined to think that (a) is the correct assumption. – ocap Aug 24 '22 at 15:30