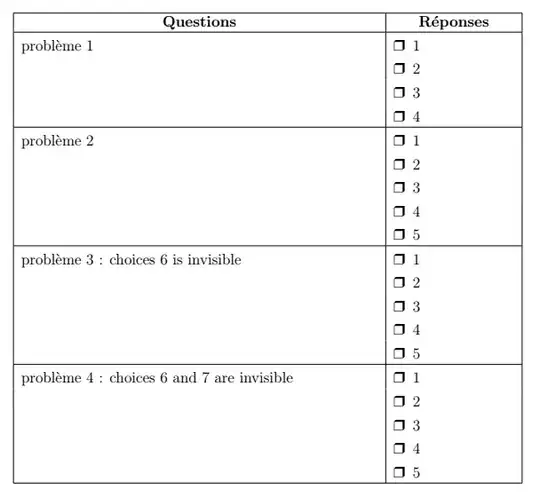
I wrote a MCQ with an unusually large number of proposed answers (7 answers). I realize that it is not possible to propose more than 5 answers to a question. How can the MCQ be able to offer more than 5 answers?
\documentclass[a4paper, 12pt,french]{article} % Présentation générale et mise en page
\usepackage[margin=5mm]{geometry}
\usepackage{siunitx}
\sisetup{locale=FR}
\usepackage[right]{eurosym}
%macro from https://tex.stackexchange.com/questions/440382/package-eurosym-how-to-change-the-decimal-separator
\makeatletter
\renewcommand{\EUR}[2][]{%
\if@EURleft\euro\,\fi
\num[#1]{#2}%
\if@EURleft\else\,\euro\fi
}
\makeatother
\usepackage{alterqcm}
\begin{document}
\begin{minipage}{.7\textwidth}
\begin{alterqcm}[lq=.7\columnwidth,num=false,symb = \dingsquare]
\AQquestion{problème 1}{%
{1},
{2},
{3},
{4}}
\AQquestion{problème 2}{%
{1},
{2},
{3},
{4},
{5}}
\AQquestion{problème 3 : choices 6 is invisible}{%
{1},
{2},
{3},
{4},
{5},
{6}}
\AQquestion{problème 4 : choices 6 and 7 are invisible}{%
{1},
{2},
{3},
{4},
{5},
{6},
{7}}
\end{alterqcm}
\end{minipage}
\end{document}