How to Generate Perpendicular Bisectors in Graphs Using Tkz-Graph

Question

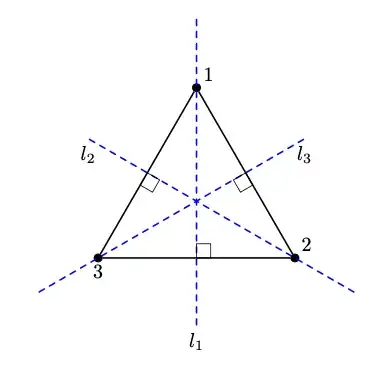
I am trying to demonstrate a geometric way to determine the symmetries of a graph generated using tkz-graph.

I was able to use a not-so-elegant way to get one of the perpendicular bisectors. How may I generate the other ones without figuring out the coordinates they would pass through?

Also, how could I add curved arrows between the vertices to illustrate the rotational symmetries.

Here is what I have so far.

\documentclass{article}
\usepackage{pgf,tikz}
\usepackage{tkz-graph}
\begin{document}
    \begin{tikzpicture}[scale=1.75,rotate=90]
        \draw[dashed,blue,thick] (1.5,0) -- (-1,0) node[below] {$l_1$};
        \GraphInit[vstyle=Classic]
        \begin{scope}[VertexStyle/.append style = {minimum size = 4pt, inner sep = 0pt}]
            \Vertices[ Math, Lpos=90]{circle}{1,3,2}
            \Edges(1,3,2,1)
        \end{scope}
    \end{tikzpicture}
\end{document}

Answer 1

The perpendicular bisectors can be made with e.g. tkz-euclide(same author - Alain Matthes as tkz-graph).

A figure like this would better be made purely in tkz-euclide, but they can be mixed. This code can be improved in many ways:

\documentclass[tikz, border=1cm]{standalone}
\usepackage{tkz-graph, tkz-euclide}
\begin{document}
\begin{tikzpicture}
\GraphInit[vstyle=Classic]
\tikzset{VertexStyle/.append style={minimum size=4pt, inner sep=0pt}}
\SetGraphUnit{2}
\begin{scope}[rotate=90]
\SetVertexNoLabel
\Vertices{circle}{A,B,C}
\end{scope}
\Edges(A,B,C,A)
\node[above right] at (A) {$1$};
\node[below] at (B) {$3$};
\node[above right] at (C) {$2$};
\tkzDefLinemediator
\tkzGetPoints{P}{Q}
\tkzDrawLinesdashed, blue, thick, add=0.2 and -0.3
\tkzLabelLinebelow, pos=0.7{$l_2$}
\tkzDefMidPoint(A,B)
\tkzGetPoint{M}
\tkzMarkRightAngle(P,M,B)
\tkzDefLinemediator
\tkzGetPoints{P}{Q}
\tkzDrawLinesdashed, blue, thick, add=0.2 and -0.3
\tkzLabelLinebelow, pos=0.7{$l_1$}
\tkzDefMidPoint(B,C)
\tkzGetPoint{M}
\tkzMarkRightAngle(P,M,C)
\tkzDefLinemediator
\tkzGetPoints{P}{Q}
\tkzDrawLinesdashed, blue, thick, add=0.2 and -0.3
\tkzLabelLinebelow, pos=0.7{$l_3$}
\tkzDefMidPoint(C,A)
\tkzGetPoint{M}
\tkzMarkRightAngle(P,M,C)
\end{tikzpicture}
\end{document}