I am trying to demonstrate a geometric way to determine the symmetries of a graph generated using tkz-graph.
I was able to use a not-so-elegant way to get one of the perpendicular bisectors. How may I generate the other ones without figuring out the coordinates they would pass through?
Also, how could I add curved arrows between the vertices to illustrate the rotational symmetries.
Here is what I have so far.
\documentclass{article}
\usepackage{pgf,tikz}
\usepackage{tkz-graph}
\begin{document}
\begin{tikzpicture}[scale=1.75,rotate=90]
\draw[dashed,blue,thick] (1.5,0) -- (-1,0) node[below] {$l_1$};
\GraphInit[vstyle=Classic]
\begin{scope}[VertexStyle/.append style = {minimum size = 4pt, inner sep = 0pt}]
\Vertices[ Math, Lpos=90]{circle}{1,3,2}
\Edges(1,3,2,1)
\end{scope}
\end{tikzpicture}
\end{document}
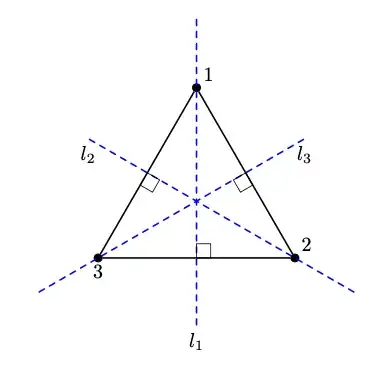
rotate, andreflect(a built-in in Asymptote, but not in TikZ). Essence of the figure is not about perpendicular bisectors – Black Mild Oct 07 '22 at 22:12