I want to show off a more automatic approach on making such a table.
While I still think, it won't hurt anyone using an external tool to calculate the values and just pasting them into your document, we can also let them be calculated
- by PGFmath (with bad precision),
- by the PGF library
fpu (with still bad precision),
- with the L3
xfp package (see Rmano's answer) (or similar packages) or, for example,
- with Lua when using LuaLaTeX.
Either way you choose you're going to adjust the \prntFormula macro a bit.
With PGFmath or the fpu library, it's
\newcommand*\prntFormula[1]{\pgfmathparse{#1}\pgfmathprintnumber{\pgfmathresult}}
With Lua, it's
\renewcommand*\prntFormula[1]{%
\edef\pgfmathresult{\directlua{tex.print(#1)}}\pgfmathprintnumber{\pgfmathresult}}
while is what I'm using here. I have defined some shortcuts so that I can use the same function names as with PGFmath.
With the xfp package, you will need to smuggle a d in since the normal functions default to radians.
Looks like Lua supports a precision of 15 digits which is what I will be using here. Not that anyone needs that many digits …
Code
\documentclass[border=5pt,tikz]{standalone}
\makeatletter
\newcommand*\repeatMe[2]{\ifnum#1=0 \expandafter\@gobble\else\expandafter\@firstofone\fi{#2\expandafter\repeatMe\expandafter{\the\numexpr#1-1\relax}{#2}}}
\makeatother
\newcommand*\prntFormula[1]{\pgfmathparse{#1}\pgfmathprintnumber{\pgfmathresult}}
%% Or with Lua:
\pgfkeys{/make lua shortcut/.code args={#1=#2}{\directlua{#1 = function (x) return #2(math.rad(x)) end}},
/make lua shortcut/.list={sin=math.sin, cos=math.cos, tan=math.tan, cot=1/math.tan}}
\renewcommand*\prntFormula[1]{\edef\pgfmathresult{\directlua{tex.print(#1)}}\pgfmathprintnumber{\pgfmathresult}}
%%
\usetikzlibrary{arrows.meta,matrix}
\begin{document}
\begin{tikzpicture}[
arrows={[scale=.6667]},
tight matrix/.style={every outer matrix/.append style={inner sep=+0pt}},
precision/.style args={#1.#2}{number format={precision={#2}}, text width=width("\repeatMe{#1}{0}\ifnum#2>0 .\fi\repeatMe{#2}{0}")},
nc/.code=\def\nc{#1}, % "node contents"
columns/.style 2 args={/utils/tempa/.style={column ##1/.append style={#2}},/utils/tempa/.list={#1}},
rows/.style 2 args ={/utils/tempa/.style={row ##1/.append style={#2}}, /utils/tempa/.list={#1}},
range lists/.style args={rows#1columns#2=#3}{/utils/tempa/.style={/utils/tempb/.style={row ##1 column ####1/.append style={#3}},/utils/tempb/.list={#2}},/utils/tempa/.list={#1}},
/pgf/number format/.code=\pgfqkeys{/pgf/number format}{#1}]
\newcommand*\nc{}% default value
\newcommand*\currentx{\the\numexpr\the\pgfmatrixcurrentrow-2\relax}
\newcommand*\reversex{\the\numexpr90-\currentx\relax}
\matrix[
ampersand replacement=\&, matrix of math nodes, tight matrix, inner xsep=\tabcolsep,
number format={fixed, fixed zerofill=true},
cells = {align=right, precision=1.3, text height=height("0")},
columns = {1,6} {text width=width("00")},
columns = {2} {cyan, nc=\prntFormula{sin(\currentx)}, precision=1.14},
columns = {3} {magenta, nc=\prntFormula{cos(\currentx)}, precision=1.14},
columns = {4} {blue, nc=\prntFormula{tan(\currentx)}, precision=1.14},
columns = {5} {violet, nc=\prntFormula{cot(\currentx)}, precision=2.13},
rows = {1} {align=center, nodes={fill=gray!40}},
rows = {48} {align=center, nodes={fill=red!20}},
range lists = {rows 2,...,47 columns 1 = nc=\currentx, nodes={fill=gray!40}},
range lists = {rows 2,...,47 columns 6 = nc=\reversex, nodes={fill=red!20}},
range lists = {rows 2 columns 5 = nc=\infty, align=center},
range lists = {rows 3,...,7 columns 5 = precision=2.12, execute at end node=\hphantom{0}}
] (m) {
x \& \sin x \& \cos x \& \tan x \& \cot x \& {} \\
\repeatMe{46}{||\currentx \& ||\nc \& ||\nc \& ||\nc \& ||\nc \& ||\reversex \\}
{} \& \cos x \& \sin x \& \cot x \& \tan x \& x \\ };
\draw[line width=2pt, Latex-Latex] (m-47-2.south west) |- (m-2-5.north east);
\draw[line width=2pt, Latex-Latex] (m-47-2.south west) -| (m-2-5.north east) [red];
\end{tikzpicture}
\end{document}
Output
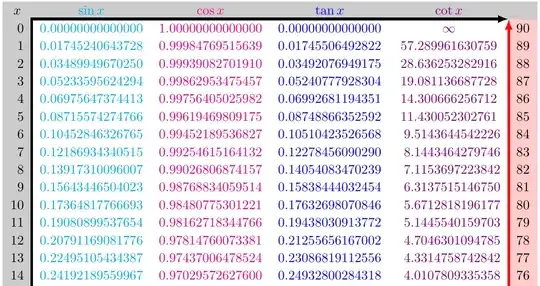


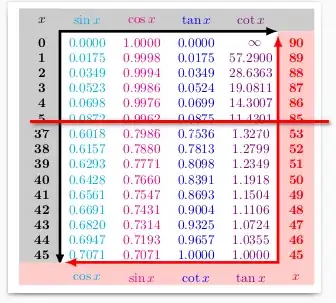
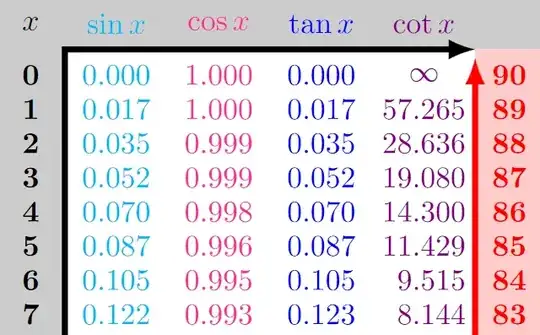

\dimenarithmetic, I doubt any of the values are accurate to 4dp – David Carlisle Oct 14 '22 at 09:45