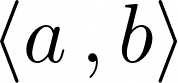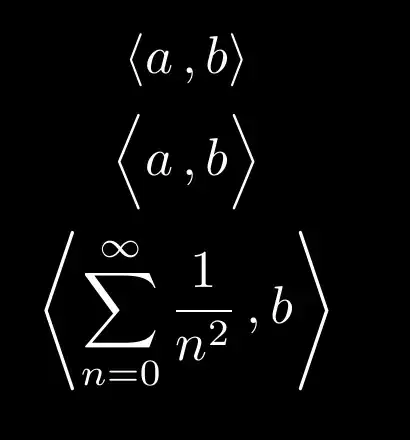Recommended way to pass all command arguments as a list

Question

I have been going from thread to thread for a while and I still cannot wrap my head around my problem.

I want to do something that I thought would be basic; declare an "inner product" command that takes two mandatory arguments and print them between brackets. Something like

Now, a simple way to do so is

\NewDocumentCommand\innerproduct{mm}{\left\langle{#1}\,,{#2}\right\rangle}

so I can get the example by doing \innerproduct{a}{b}. But \innerproduct{a,b} would be much nicer, and that is where I am not sure how to proceed. I read about argument processors and I tried

\NewDocumentCommand\privateip{mm}{\left\langle{#1}\,,{#2}\right\rangle}
\NewDocumentCommand\innerproduct{>{\SplitArgument{1}{,}}m}{\privateip#1}

which does the job but seems a bit shaky for me, in the sense that I would rather not have to define two commands each time that I want to accomplish this. Can the two be bundled together?

There are examples around doing all sorts of cool stuff by iterating over lists in a (to me) obscure manner, but I think what I want is much simpler: making sure the two arguments are present, and being able to access them to print them.

---

EDIT: Thanks for the many answers!

To clarify a little bit, my concern was not about having to define a chain of commands to achieve my results, but the cluttered namespace. And my example was simple, but I hoped I could generalise the answer to other cases.

I did not know about mathtools and I liked that approach, which indeed fills perfectly this use case. I'll also check out semantex in the future. That is where I am at now:

\makeatletter
\DeclarePairedDelimiterXPP\p@ip[3]{}\langle\rangle{\ifblank{#3}{}{_#3}}{#1\,,#2}
    \NewDocumentCommand\innerproduct{so>{\SplitArgument{1}{,}}mO{}}{%
        \IfBooleanTF{#1}{%
            \p@ip*#3{#4}%
        }{%
            \IfNoValueTF{#2}{\p@ip#3{#4}}{\p@ip[#2]#3{#4}}%
        }%
    }
\makeatother

I do not how I missed it, but I used some @ magic to get on with my clutter problem. The optional star or size argument can be used normally, I get the target behaviour \innerproduct{a,b}, and I added an optional suffix that I need to distinguish operators (that will demand some spacing tuning, but that is another problem). Hooray!

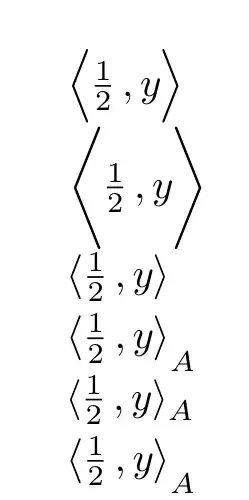
$\innerproduct[\Big]{\frac12,y}$
$\innerproduct[\Bigg]{\frac12,y}$
$\innerproduct*{\frac12,y}$
$\innerproduct*{\frac12,y}[A]$
$\innerproduct{\frac12,y}[A]$
$\innerproduct[\big]{\frac12,y}[A]$

Still keen on any comments.

Answer 1

In your case, just define

\DeclarePairedDelimiter{\innerproduct}{\langle}{\rangle}

and you're done, because if you input

\innerproduct{a,b}

the argument is already in the expected form. There's no need to split a comma separated list in order to just rebuild it.

But… Yes, there's more. Suppose your coauthor is fond of the “bra-ket” notation loved by physicists and you don't want or can't argue about the choice. Your text is already full of \innerproduct{a,b} or maybe \innerproduct[\Big]{x,y} (where x,y requires \Big, of course) and you don't want to afford the burden of changing everything in some way or another.

OK, now we can solve the issue in a very simple way. We still use the infrastructure of mathtools, but need the more advanced \DeclarePairedDelimiterX and also \NewDocumentCommand.

\DeclarePairedDelimiterX{\innerproduct}[1]{\langle}{\rangle}{\makebraket{#1}}
\NewDocumentCommand{\makebraket}{>{\SplitArgument{1}{,}}m}{\makebraketaux#1}
\NewDocumentCommand{\makebraketaux}{mm}{#1\;\delimsize\vert\;#2}

So \innerproduct essentially does the same as before, but it will also delegate to \makebraket the processing of the argument given as a comma separated list (of two items).

With >{\SplitArgument{1}{c}}m, the given argument a,b will be handed to the following code as {a}{b} and so we must define \makebraketaux to have two arguments.

Full example:

\documentclass{article}
\usepackage{mathtools}
% my preferred way, but my coauthor doesn't like it :-(
% \DeclarePairedDelimiter{\innerproduct}{\langle}{\rangle}
% here's for the bra-ket way
\DeclarePairedDelimiterX{\innerproduct}[1]{\langle}{\rangle}{\makebraket{#1}}
\NewDocumentCommand{\makebraket}{>{\SplitArgument{1}{,}}m}{\makebraketaux#1}
\NewDocumentCommand{\makebraketaux}{mm}{#1;\delimsize\vert;#2}
\begin{document}
[
\innerproduct{a,b}
\quad
\innerproduct[\big]{a,b}
\quad
\innerproduct[\Big]{\frac{x}{2},\frac{y}{2}}
\quad
\innerproduct[\bigg]{\frac{x}{2},\frac{y}{2}}
\quad
\innerproduct*{\frac{x}{2},\frac{y}{2}}
]
\end{document}

If you're concerned with the deluge of macros, don't. TeX programming usually requires this either to simplify the code or because the auxiliary macro cannot be avoided (recursion, for instance). Take >{\SplitArgument{1}{,}} as an example of the latter case and don't worry: cascading macros are normal staple food for TeX programmers.

Now, it turns out I overlooked your requirement, but that's essentially the same as in the \makebraket part.

\documentclass{article}
\usepackage{mathtools}
\DeclarePairedDelimiterX{\innerproduct}[1]{\langle}{\rangle}{\addthinspace{#1}}
\NewDocumentCommand{\addthinspace}{>{\SplitArgument{1}{,}}m}{\addthinspaceaux#1}
\NewDocumentCommand{\addthinspaceaux}{mm}{#1,,#2}
\begin{document}
[
\innerproduct{a,b}
\quad
\innerproduct[\big]{a,b}
\quad
\innerproduct[\Big]{\frac{x}{2},\frac{y}{2}}
\quad
\innerproduct[\bigg]{\frac{x}{2},\frac{y}{2}}
\quad
\innerproduct*{\frac{x}{2},\frac{y}{2}}
]
\end{document}

A version with (almost) no auxiliaries:

\DeclarePairedDelimiterX{\innerproduct}[1]{\langle}{\rangle}{\addthinspace{#1}}
\ExplSyntaxOn
\NewDocumentCommand{\addthinspace}{m}
 {
  \clist_use:nn { #1 } { ,, }
 }
\ExplSyntaxOff

Answer 2

If you decide to put the list into {...} then two macros are needed because TeX is able to read the parameter encapsulated in {...} by a macro only as indivisible object. The outer macro can put it as a parameter of another inner macro without {...} and the second macro is able to read parameters separated by given tokens. It means:

% usage \innerproduct{a,b}
\def\innerproduct #1{\innerproductA #1\relax}
\def\innerproductA #1,#2\relax{\left\langle{#1}\,,{#2}\right\rangle}

If you decide to use another symbols for denoting your parameters than you have no problem and you can define only single macro. For example:

% usage \innerproduct <a,b>
\def\innerproduct <#1,#2>{\left\langle{#1}\,,{#2}\right\rangle}

Answer 3

At first it may seem silly to use two commands to do something relatively simple, but this way has its advantages. There is a document level command that the user will use and it will always be used the same way, namely in this case to supply a list of two items separated by a comma. This small list is then passed to an inner command defined by the programming layer that actually implements the desired formatting. The details are hidden from the document level command, meaning that the implementation can be modified with no changes to how the command is used in a document.

Here is an example showing one way to implement your inner product example using the L3 programming layer. I assume an up to date TeX Live distribution, and I include comments that I hope make everything understandable.

% !TEX program = lualatexmk
% !TEX encoding = UTF-8 Unicode
\documentclass{article}
\ExplSyntaxOn
% Document level command
\NewDocumentCommand{\InnerProduct}{ m }
  {
    __aubergine_innerproduct:n { #1 }
  }%
% Programming layer command.
% Define a new sequence.
\seq_new:N \l__aubergine_vectorarg_seq
% Define a new function that takes one argument, which
% is a sequence of two items separated by a comma.
\cs_new_protected:Npn __aubergine_innerproduct:n #1
  {
    % Split the sequence into individual items delimited
    % by the comma.
    \seq_set_split:Nnn \l__aubergine_vectorarg_seq {,} { #1 }
    % Format the items one at a time between angle brackers
    % and again separated by a comma and a space.
    \langle \seq_use:Nn \l__aubergine_vectorarg_seq { , , } \rangle
  }
\ExplSyntaxOff
\begin{document}
( \InnerProduct{a,b} )
[
  \InnerProduct{c,d}
]
\end{document}

Answer 4

My package semantex was built more or less specifically for these kinds of constructions:

\documentclass{article}
\usepackage{semantex}
\NewVariableClass\MyVar
\NewObject\MyVar\innerproduct[
    left par=\langle,
    right par=\rangle,
    set arg sep={,,},
]
\begin{document}
\begin{gather}
    \innerproduct{a,b}
\
    \innerproduct[par=\Big]{a,b}
\
    \innerproduct[par=auto]{
        \sum_{n=0}^{\infty} \frac{1}{n^2} ,
        b
    }
\end{gather}
\end{document}

Answer 5

Fundamentally TeX has a lot of limitations as a programming language. So usually to implement some feature it's mandatory to define auxiliary commands to do the task.

It's not visible to you, but \NewDocumentCommand itself, when called like \NewDocumentCommand\innerproduct, defines (at least, I don't really remember the details) two commands, one being the \innerproduct itself and one has the "special" name \innerproduct code (it's nontrivial to access this one directly, you need some TeX knowledge.)

(technical note: you can cut down on the number of hash table entries by defining them "on demand", but fundamentally it makes little difference.)

Anyway, I think what you want is just to make the code uncluttered. That can be done with an auxiliary macro like this...

\documentclass{article}
% ======== begin magic ========
\ExplSyntaxOn
% #1: the command, #2: the body
\cs_new_protected:Npn \NewDocumentCommandTwoCommaSeparatedArgs #1 #2 {
    \exp_args:Nc __aubergine_ndccomma_aux:NNn {\cs_to_str:N #1 ~ private} #1 {#2}
}
% #1: the private control sequence, #2: the command, #3: the body
\cs_new_protected:Npn __aubergine_ndccomma_aux:NNn #1 #2 #3 {
    \cs_new_protected:Npn #1 ##1 ##2 {#3}
    \NewDocumentCommand#2{>{\SplitArgument{1}{,}}m}{#1##1}
}
\ExplSyntaxOff
% ======== end magic ========
% then you can simply do this. It "looks like" only one command definition, but is actually at least three.
\NewDocumentCommandTwoCommaSeparatedArgs\innerproduct{\left\langle{#1},,{#2}\right\rangle}
\begin{document}
$\innerproduct{a, b}$
\end{document}

The output is what you expect.

Answer 6

With a suitable superhero theme song playing in the background, this is a job for mathtools! This package provides the \DeclarePairedDelimiterX command that exsists precisely for defining commands like these. By defining

\DeclarePairedDelimiterX\innerproduct[2]{\langle}{\rangle}{#1\,, #2}

the command $\innerproduct{a}{b}$ is the same as $\langle a,b\rangle$. This does not answer your question but, rather, gives another way of doing what you already have. An easy way to give something closer to what you are actually asking for is to define

\DeclarePairedDelimiterX\innerproduct[1]{\langle}{\rangle}{#1}

and now $\innerproduct{a,b}$ does do what you want, but without actually splitting up the two inputs in the inner product, which isn't strictly necessary in this example.

If you want to do this "properly" then, as explained below, we need a helper command that "splits" the input. As the OP says, this can be done using the \SplitArgument command from the xparse package. If we rename the first command above \realInnerProduct and define

\NewDocumentCommand\innerproduct{>{\SplitArgument{1}{,}}{m}}
{
    \realInnerProduct#1
}

then \innerproduct{a,b} does what the OP asks for. Of course, this uses two commands, whereas the OP asks for one.

This works but it you have to ask why we are using \DeclarePairedDelimiterX at all because it looks like a lot of extra bother without much gain. The point is that this command has built in mechanisms for resizing delimiters. By using \SplitArgument, as above, we have "lost" this extra functionality because \realInnerProduct is burried inside the definition of \innerproduct. We can regain the ability to resize the delimiters by adding an optional argument to the \innerproduct command. If we do this then we can, for example, type $\innerproduct[\Big]{\sum_{i=1}^n v_i,b}$ to produce:

That is, our inner product produces different sized angle brackets when we add \big, \Big, ... as an optional argument.

Here is the full code:

\documentclass{amsart}
\usepackage{xparse}
\usepackage{mathtools}
\NewDocumentCommand\innerproduct{o>{\SplitArgument{1}{,}}{m}}{
  \IfNoValueTF{#1}{\realInnerProduct#2}{\realInnerProduct[#1]#2}
}
\DeclarePairedDelimiterX\realInnerProduct[2]{\langle}{\rangle}{#1,, #2}
\begin{document}
$\innerproduct{a,b}$
$\innerproduct[\Big]{\sum_{i=1}^n v_i,b}$
\end{document}

OK, this is how I would (and have) defined these commands but the OP really asks for a way to do this using one command. As the question is posed, this is not really possible because given \innerproduct{a,b} we have a command that accepts one argument, namely a,b, so we need a second command to break a,b into its' two components. We need these extra commands whether we do this by introducing a second helper command, or by using some other whiz bang features of LaTeX inside our single command.

It is relatively easy to define a command so that \innerproduct a,b expands to \langle a, b\rangle. For example,

\def\innerproduct#1,#2{\langle#1,#2\rangle}

will do this. This is NOT a good solution, however, because we would need extra braces for expressions like \innerproduct a, {\sum_{i=1}^nv_i} -- although, \innerproduct \sum_{i=1}^nv_i,b would be fine. Similar to the LaTeX3 solutions above, we could instead define

\usepackage{expl3}
\ExplSyntaxOn
\NewDocumentCommand\innerproduct{m}
{
  \clist_set:Nn \l_tmpa_clist {#1}
  \langle \clist_use:Nn \l_tmpa_clist {\, ,} \rangle
}
\ExplSyntaxOff

which is a "one command" solution. Of course, as soon as you start using packages like xparse, mathtools, LaTeX3, or ..., even a "one command" solution typically involves many other commands that you are using without realising it. In this case, many LaTeX users will have no idea what the code above does, even though it is quite simple:

• \clist_set:Nn breaks #1 into a comma separated list, which is stored in \l_tmpa_clist
• \clist_use:Nn spits the list out again, separating the items by \, , and sandwiched between \langle ... \rangle.

This version of the \innerproduct command will work with a comma separated list of arbitrary length, but it will not resize the delimiters. Personally, I prefer the solution above that uses \DeclarePairedDelimiterX.