I'd argue this is due to TeX/PGFMath's imprecision, if we do
\documentclass[tikz]{standalone}
\tikzset{declare function={infty(\x)=sqrt(-1/2-\x*\x+sqrt(1/4+2*\x*\x));}}
\begin{document}
\tikz[domain=-1:1, scale=5, samples=100]
\draw plot ([/utils/exec=\pgfmathparse{infty(\x)}\typeout{\x => \pgfmathresult}]
\x,{ infty(\x)});
\end{document}
the log file will contain
-1.0 => 0.00000
-0.998 => 0.03646
-0.996 => 0.05157
-0.994 => 0.06300
-0.992 => 0.07252
-0.99 => 0.08099
⋮ ⋮
-0.00655 => 0.00447
-0.00455 => 0.00000
-0.00255 => 0.00000
-0.00055 => 0.00000
0.00145 => 0.00000
0.00345 => 0.00447
⋮ ⋮
0.9909 => 0.07733
0.9929 => 0.06841
0.9949 => 0.05805
0.9969 => 0.04538
0.9989 => 0.02701
Dividing the range -1:1 in 1001 pieces is not a good exercise for PGFMath/TeX.
The quickest fix for this would be to use samples at as such:
\tikz[domain=-1:1, scale=5, samples at={-500,...,500}]
\draw plot (\x/500,{ infty(\x/500)});
TeX/\foreach is very good at incrementing an integer:
-1.0 => 0.00000
-0.99799 => 0.03660
-0.99599 => 0.05157
-0.99399 => 0.06300
⋮ ⋮
-0.006 => 0.00447
-0.004 => 0.00000
-0.002 => 0.00000
0.0 => 0.00000 ← symmetry!
0.002 => 0.00000
0.004 => 0.00000
0.006 => 0.00447
⋮ ⋮
0.99199 => 0.07266
0.99399 => 0.06300
0.99599 => 0.05157
0.99799 => 0.03660
1.0 => 0.00000
As with all things computer, even TeX works in powers of 2, so a number like 1025 work, too. (With a sample count of n the domain will be divided into n − 1 parts.)
You can also side-step the problem by concatenating another plot with domain 1:-1 so that the point at x = 1 will be calculated explicitly and ending the path with -- cycle to get back to (-1, 0).
Of course, there's the fpu library, gnuplot and other external tools.
But I've also added a bit complexer solution that draws your symbol cleaner, in my opinion – and with less points!
Code
\documentclass[tikz]{standalone}
\tikzset{declare function={infty(\x)=sqrt(-1/2-\x*\x+sqrt(1/4+2*\x*\x));}}
\begin{document}
\tikz[domain=-1:1, scale=5]
\draw plot[domain=-1:1, samples at={-500,...,500}] (\x/500,{ infty(\x/500)})
-- plot[domain=1:-1, samples at={500,...,-500}] (\x/500,{-infty(\x/500)}) -- cycle;
\tikz[domain=-1:1, scale=5, samples=1025]{
\draw plot (\x, { infty(\x)});
\draw plot (\x, {-infty(\x)});
}
\tikz[scale=5, samples=1000]
\draw plot[domain=-1:1] (\x, { infty(\x)})
-- plot[domain=1:-1] (\x, {-infty(\x)})
-- cycle;
\tikz[scale=5]
\draw plot[domain=-1:0, samples at={-500,...,-300,-295,-290,...,0}] (\x/500, { infty(\x/500)})
-- plot[domain= 0:1, samples at={0, 5,..., 300, 301, 302,..., 500}] (\x/500, {-infty(\x/500)})
-- plot[domain= 1:0, samples at={ 500,..., 300, 295, 290,...,0}] (\x/500, { infty(\x/500)})
-- plot[domain=0:-1, samples at={0,-5,...,-300,-301,-302,...,-500}] (\x/500, {-infty(\x/500)})
-- cycle;
\end{document}
Output
(The detail is in the crossing.)
1, 2:
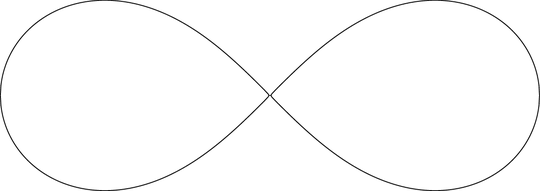
3:
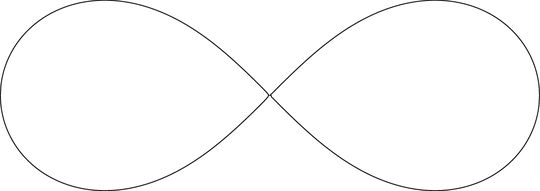
4:
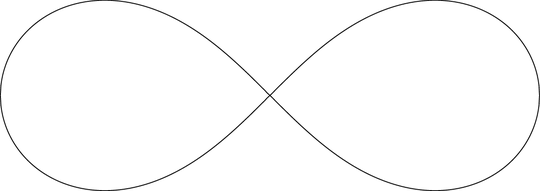





\xthat will be used is0.9989(→ y = 0.02701). I'd insert(1, 0)manually. – Qrrbrbirlbel Oct 27 '22 at 18:51samples=1024and you will see the gap disappears. – Thruston Oct 27 '22 at 19:08