2

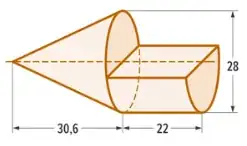
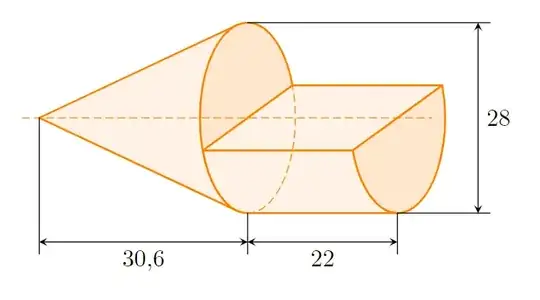
Here is a nice way to make some 3d objects, but I've failed to find a way to connect two 3d objects into single one object like this one (also it would be nice to know how to add arrows with numbers):

two 3d objects connected

This is the MWE I've tried so far (just copied the code and removed some parts). I have no idea how to rotate them, also how to draw half cylinder. I don't even know if that's the right direction to go. But the main problem is connecting 3d objects, if that's possible.

\documentclass[11pt]{scrartcl} 
\PassOptionsToPackage{dvipsnames,svgnames}{xcolor}     
\usepackage{xkeyval,tkz-base}
\usetikzlibrary{arrows,calc}
 \makeatletter%

\define@cmdkey[TKZ]{ell}{color}{}
\define@cmdkey[TKZ]{ell}{shift}{}

\presetkeys[TKZ]{ell}{color = {},shift = 0}{}


\newcommand*{\ellipseThreeD}[1][]{\tkz@ellipseThreeD[#1]}% 
\def\tkz@ellipseThreeD#1(#4,#5){%
\setkeys[TKZ]{ell}{#1}%
  \draw[yshift=\cmdTKZ@ell@shift cm,dashed] (#4,0) arc(0:180:#4 and #5);
  \draw[yshift=\cmdTKZ@ell@shift cm ] (-#4,0) arc(180:360:#4 and #5); 
  \path[fill=\cmdTKZ@ell@color,opacity=0.5,shade](#2 cm,#3 cm) ellipse (#4 and #5);

}


\def\tkzCone{\pgfutil@ifnextchar[{\tkz@cone}{\tkz@cone[]}} 
\def\tkz@cone[#1]#2#3#4{%


\pgfmathsetmacro{\bb}{#2#3}

\pgfmathsetmacro{\yy}{\bb\bb/#4}

\pgfmathsetmacro{\xx}{#2*sqrt((1-\yy)/#4)} 
\fill[color=Maroon!10] (0,#4)--(-\xx,\yy)  arc(180:360:\xx cm and .5 cm); 
\ellipseThreeDcolor=Maroon!30(\xx cm,.5 cm)
\draw (0,#4)--(\xx,\yy);
\draw (0,#4)--(-\xx,\yy); 
}%


\def\tkzCylinder{\pgfutil@ifnextchar[{\tkz@cylinder}{\tkz@cylinder[]}} 
\def\tkz@cylinder[#1]#2#3#4{% 
\pgfmathsetmacro{\bb}{#2#3}

\pgfmathsetmacro{\yy}{\bb\bb/#4}

\pgfmathsetmacro{\xx}{#2*sqrt((1-\yy)/#4)}
  \fill[color=Maroon!10] (-\xx cm,0)--(-\xx cm,#4 cm)

         arc(180:360:\xx cm and .5 cm)--(\xx cm,0) 
         arc(360:180:\xx cm and .5 cm);

\ellipseThreeDcolor=Maroon!30(\xx cm,.5 cm)
\begin{scope}[yshift=#4 cm]
  \drawfill=\cmdTKZ@ell@color,opacity=0.5,shade ellipse (\xx cm and .5 cm) ;

\end{scope}
\draw (\xx cm,0)--(\xx cm,#4 cm);
\draw (-\xx cm,0)--(-\xx cm,#4 cm); 
}%


\begin{document}


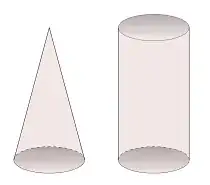
\tikz  \tkzCone{3}{0}{5};
  \hspace{1cm}
 \tikz   \tkzCylinder{3}{0}{5};


\end{document}

It produces this:

enter image description here

Black Mild
  • 17,569
Robai
  • 185

2 Answers2

3

I would probably just draw it like this (thanks to this answer for the hint about how to calculate the critical angle):

\documentclass[border=10pt]{standalone} 
\usepackage{tikz}

\begin{document}


\begin{tikzpicture}[>=stealth, line join=round, line cap=round]


% define tilt angle
\pgfmathsetmacro{\TiltAngle}{20}


% CONE
% calculate critical angle where tangentials intersect ellipsis
\pgfmathsetmacro{\ConeHeight}{3.06} 
\pgfmathsetmacro{\ConeRadius}{1.4}
\pgfmathsetmacro{\CritAngle}{acos((\ConeRadius/2)/\ConeHeight)}


% draw tangentials
\draw[thick, orange, fill=orange!10]
    ({180-\CritAngle}:{\ConeRadius/2} and {\ConeRadius}) 
        -- ({-\ConeHeight},0) coordinate (A)
        -- ({180+\CritAngle}:{\ConeRadius/2} and {\ConeRadius});
% draw visible part of base
\draw[thick, orange, fill=orange!20] 
    (270:{\ConeRadius/2} and {\ConeRadius}) coordinate (B)
        arc[start angle=270, end angle=\TiltAngle, 
            x radius={\ConeRadius/2}, y radius={\ConeRadius}];
\coordinate (E) at (90:{\ConeRadius/2} and {\ConeRadius});


% HALF CYLINDER
\pgfmathsetmacro{\CylinderHeight}{2.2}


% draw base
\draw[thick, orange, fill=orange!20]
    ([shift={(right:\CylinderHeight)}]\TiltAngle:{\ConeRadius/2} and {\ConeRadius}) 
        arc[start angle={\TiltAngle}, end angle={-(180-\TiltAngle)}, 
            x radius={\ConeRadius/2}, y radius={\ConeRadius}];
% draw bottom part
\draw[thick, orange, fill=orange!10] 
    ({180+\TiltAngle}:{\ConeRadius/2} and {\ConeRadius}) 
        arc[start angle={180+\TiltAngle}, end angle=270, 
            x radius={\ConeRadius/2}, y radius={\ConeRadius}]
        -- ++(\CylinderHeight,0) coordinate (C)
        arc[start angle=270, end angle={180+\TiltAngle}, 
            x radius={\ConeRadius/2}, y radius={\ConeRadius}];
% draw cut surface
\draw[thick, orange, fill=orange!10] 
    (\TiltAngle:{\ConeRadius/2} and {\ConeRadius}) 
        -- ({180+\TiltAngle}:{\ConeRadius/2} and {\ConeRadius}) 
        -- ++(\CylinderHeight,0)
        -- ([shift={(right:\CylinderHeight)}]\TiltAngle:{\ConeRadius/2} and {\ConeRadius}) 
        -- cycle;


% draw hidden part of cone base
\draw[densely dashed, orange] 
    (270:{\ConeRadius/2} and {\ConeRadius}) 
        arc[start angle=-90, end angle=\TiltAngle, 
            x radius={\ConeRadius/2}, y radius={\ConeRadius}];


% AXIS
\draw[densely dashed, orange] ({-\ConeHeight-0.25},0) -- ({\CylinderHeight+0.5},0);


% ANNOTATIONS
\draw (A) -- ({-\ConeHeight},-2) coordinate (a);
\draw (B) -- (0,-2) coordinate (b);
\draw (C) -- (\CylinderHeight,-2) coordinate (c);
\draw (C) -- (C -| {\ConeHeight+0.5},0) coordinate (d);
\draw (E) -- (E -| {\ConeHeight+0.5},0) coordinate (e);


\draw[<->] ([yshift=5pt]a) -- ([yshift=5pt]b) node[midway, below] {30,6};
\draw[<->] ([yshift=5pt]b) -- ([yshift=5pt]c) node[midway, below] {22};
\draw[<->] ([xshift=-5pt]d) -- ([xshift=-5pt]e) node[midway, right] {28};


\end{tikzpicture}


\end{document}

enter image description here

Jasper Habicht
  • 48,848
3

My Asymptote code just uses the extrude command. The first base b1 is a circle that gives horizontal cone after extruding, while the second base b2 is a half of circle that gives horizontal half-cylinder after extruding

enter image description here

// http://asymptote.ualberta.ca/
unitsize(2mm);
import three;
currentprojection=orthographic(3,1,.6,center=true,zoom=.8);
pen p=yellow;
real r=14;
real y1=30.6,y2=22;
triple V1=(0,-y1,0),V2=(0,y2,0);
path3 b1=circle(O,r,normal=Y);
path3 b2=arc(O,(r,0,0),(-r,0,0),normal=Y)--cycle;
draw(extrude(b1,V1--cycle),p);
draw(extrude(b2,V2),p);
Black Mild
  • 17,569