1

I recently discovered tikz packages, I'm completely new to this. I started to read the manual and manage to do some very simple things, but I still have a lot of difficulty with the language.

I'm writing myself some notes on the Lebesgue Integral, and I'd like to put the figures below, but I have no idea how to plot them.enter image description here

Flor do Cerrado
  • 19

1 Answers1

5

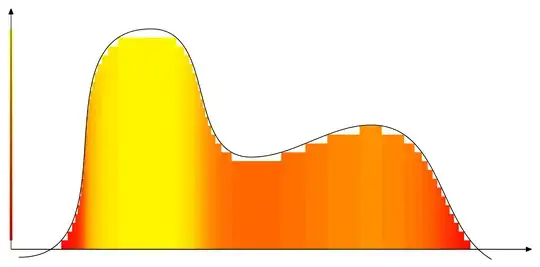
I don't know how to do this with tikz, but since you got no answers so far, I give you a start on how you can do something similar in MetaFun. This might give you an idea on how to proceed with tikz. The path fun is your function, N is the number of colors.

\startMPpage[offset=1dk]
numeric u ; u := 1cm ;
path fun ; fun := ((0.2,-0.2){right} .. 
                   (3.5,5.5){right} .. 
                   (6,2.3){right} .. 
                   (9,3.1){right} .. 
          {dir -30}(12,-0.25)) ;
numeric miny ; miny := 0 ;
numeric maxy ; maxy := ypart urcorner boundingbox fun ;
numeric N ; N := 8 ;
numeric level[] ;
rgbcolor levelcolor[] ;
path ip[] ;
path tmppath ;

for i = 1 upto N :
    level[i] := miny + (maxy - miny)*i/N ;
    message(level[i]) ;
    % levelcolor[i] := (i/N)[red,yellow] ;
    levelcolor[i] := ( uniformdeviate(1), uniformdeviate(1), uniformdeviate(1) ) ;
    ip[i] := fun firstintersectionpath ((-infinity,level[i]) -- (infinity,level[i])) ;
endfor


for i = 1 upto N :
    for j = 0 step 2 until (length(ip[i]) - 1) :
        tmppath := ( (point j of ip[i]) -- 
                     (point (j + 1) of ip[i]) -- 
                     (xpart point (j + 1) of ip[i], 0) -- 
                     (xpart point j of ip[i], 0) -- 
                     cycle ) ;
        % unfill tmppath ; % no gain
        fill tmppath scaled u withcolor levelcolor[i] ;
    endfor
    if i < N :
        draw ((0,level[i]) -- (0, level[i+1])) scaled u withpen pencircle scaled 2 withlinecap butt withcolor levelcolor[i] ;
    fi
endfor ;


draw fun scaled u ;
drawdoublearrow ( (0,6) -- origin -- (13,0) ) scaled u ;
\stopMPpage

Save the file as lebesgue.tex and run with context lebesgue.tex to get lebesgue.pdf. With N = 8 we get

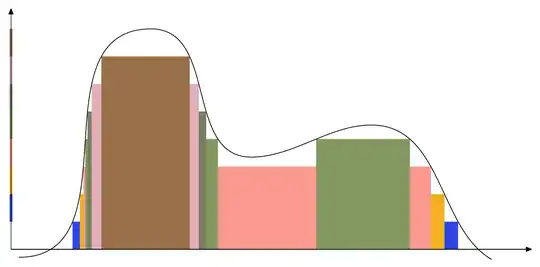
lebesgue integral

The colors are random. With N = 25 we instead get

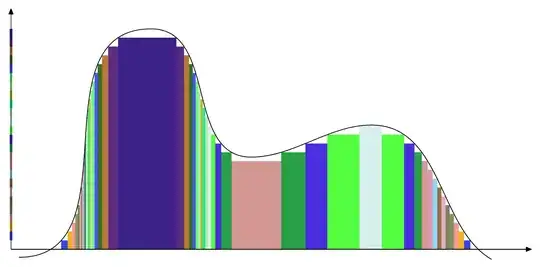
more accurate lebesgue integral

Finally, by altering the definitions of levelcolor[i], we end up with

same but with different colors

mickep
  • 8,685
  • 1
    A very minor point. But boundingbox is redundant in this numeric maxy ; maxy := ypart urcorner boundingbox fun;. You can just write maxy = ypart urcorner fun; – Thruston Dec 07 '22 at 11:13
  • True, thanks! (There are probably more possible improvements, this was merely a first try.) – mickep Dec 07 '22 at 11:17