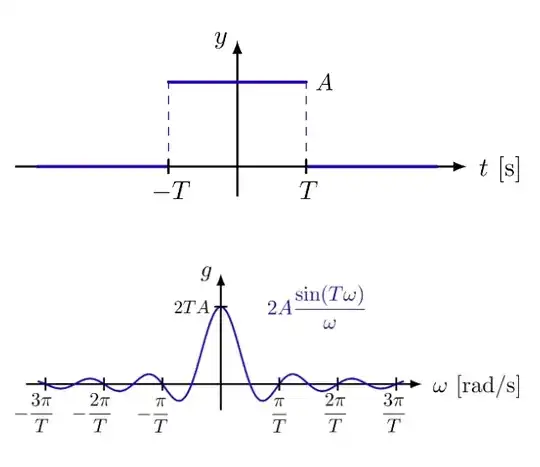
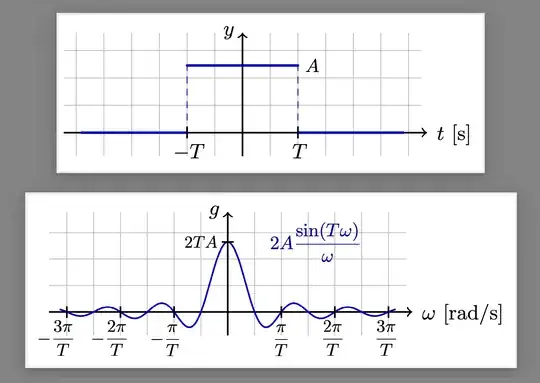
Any idea on how to elegantly put a grid behind the two functions plotted here?:
% Author: Izaak Neutelings (January 2021)
% http://pgfplots.net/tikz/examples/fourier-transform/
% https://tex.stackexchange.com/questions/127375/replicate-the-fourier-transform-time-frequency-domains-correspondence-illustrati
% https://www.dspguide.com/ch13/4.htm
\documentclass[border=3pt,tikz]{standalone}
\usepackage{amsmath}
\usepackage{tikz}
\usepackage{xcolor}
\usepackage{pgfplots}
\begin{document}
% RECTANGULAR FUNCTION
\begin{tikzpicture}
\def\xmin{-0.7\T} % min x axis
\def\xmax{3.0} % max x axis
\def\ymin{-0.4} % min y axis
\def\ymax{1.7} % max y axis
\def\A{0.67\ymax} % amplitude
\def\T{0.31*\xmax} % period
\colorlet{myblue}{blue!80!black}
\colorlet{mydarkblue}{myblue!80!black}
\tikzstyle{xline}=[myblue,thick]
\def\tick#1#2{\draw[thick] (#1) ++ (#2:0.1) --++ (#2-180:0.2)}
\tikzstyle{myarr}=[myblue!50,-{Latex[length=3,width=2]}]
\def\N{80}
\message{^^JRectangular function}
\draw[->,thick] (0,\ymin) -- (0,\ymax) node[left] {$y$};
\draw[->,thick] (-\xmax,0) -- (\xmax+0.1,0) node[below=1,right=1] {$t$ [s]};
\draw[xline,very thick,line cap=round]
({-\T},{\A}) -- ({\T},{\A}) node[black,right=0,scale=0.9] {$A$}
({-\T},0) -- ({-0.9\xmax},0)
({ \T},0) -- ({0.9\xmax},0);
\draw[xline,dashed,thin,line cap=round]
({-\T},0) --++ (0,{\A})
({ \T},0) --++ (0,{\A});
\tick{{ -\T},0}{90} node[right=1,below=-1,scale=1] {$-T$};
\tick{{ \T},0}{90} node[right=1,below=-1,scale=1] {$T$};
%\tick{0,{ \A}}{ 0} node[left=-1,scale=0.9] {$A$};
\end{tikzpicture}
% RECTANGULAR FUNCTION - frequency domain
\begin{tikzpicture}
\def\xmin{-0.7\T} % min x axis
\def\xmax{3.0} % max x axis
\def\ymin{-0.4} % min y axis
\def\ymax{1.7} % max y axis
\def\A{0.67\ymax} % amplitude
\def\T{0.31\xmax} % period
\colorlet{myblue}{blue!80!black}
\colorlet{mydarkblue}{myblue!80!black}
\tikzstyle{xline}=[myblue,thick]
\def\tick#1#2{\draw[thick] (#1) ++ (#2:0.1) --++ (#2-180:0.2)}
\tikzstyle{myarr}=[myblue!50,-{Latex[length=3,width=2]}]
\def\N{80}
\message{^^JRectangular function - frequency domain}
\def\T{0.30\xmax} % period
\def\A{0.70\ymax} % amplitude
\draw[->,thick] (0,\ymin) -- (0,\ymax) node[left] {$g$};
\draw[->,thick] (-\xmax,0) -- (\xmax+0.1,0) node[below=1,right=1] {$\omega$ [rad/s]};
\draw[xline,samples=\N,smooth,variable=\t,domain=-0.94\xmax:0.94\xmax]
plot(\t,{\Asin(360/(\T)\t)/(2pi)(\T)/\t});
\tick{{-3\T},0}{90} node[left= 5,below=-2,scale=0.85] {\strut$-\dfrac{3\pi}{T}$};
\tick{{-2\T},0}{90} node[left= 5,below=-2,scale=0.85] {\strut$-\dfrac{2\pi}{T}$};
\tick{{ -\T},0}{90} node[left= 4,below= 0,scale=0.85] {\strut$-\dfrac{\pi}{T}$};
\tick{{ \T},0}{90} node[right= 0,below= 0,scale=0.85] {\strut$ \dfrac{\pi}{T}$};
\tick{{ 2\T},0}{90} node[right=-1,below=-2,scale=0.85] {\strut$ \dfrac{2\pi}{T}$};
\tick{{ 3\T},0}{90} node[right=-1,below=-2,scale=0.85] {\strut$ \dfrac{3\pi}{T}$};
\tick{0,{\A}}{0} node[left=-1,scale=0.8] {$2TA$};
\node[mydarkblue,right,scale=0.9] at (0.2\xmax,\A)
{$2A\dfrac{\sin(T\omega)}{\omega}$}; %g(\omega) =
\end{tikzpicture}
\end{document}
Thanks for your help