Plus minus reversal in the post length decoration

Question

Why does plus and minus not work the way I expect in the post length option

\documentclass[tikz, border=1cm]{standalone}
\usetikzlibrary{decorations.pathmorphing}
\begin{document}
\begin{tikzpicture}[thick, above]
\draw[red] (0,0) --node{5cm} (5,0);
\draw[teal,
decoration={moveto, post=lineto, post length={4cm}}, decorate
] (0,-1) --node{4cm} (5,-1);
\draw[blue,
decoration={moveto, post=lineto, post length={4cm+1cm}}, decorate
] (0,-2) --node{4cm+1cm} (5,-2);
\draw[orange,
decoration={moveto, post=lineto, post length={4cm-1cm}}, decorate
] (0,-3) --node{4cm-1cm} (5,-3);
\end{tikzpicture}
\end{document}

Edit: Plus works as minus and minus works as plus in this option. My question is about why this is happening!? -And also if the behaviour can be corrected by other notation or adding extra code. A workaround is not really needed as it is simple to write plus instead of minus.

Answer 1

Try to use \dimexpr (introduced by eTeX):

\documentclass[tikz, border=1cm]{standalone}
\usetikzlibrary{decorations.pathmorphing}
\begin{document}
    \begin{tikzpicture}[thick, above]
\draw[red] (0,0) --node{5cm} (5,0);
\draw[teal,
      decoration={moveto, post=lineto, post length={4cm}}, decorate] 
       (0,-1) -- node{4cm} (5,-1);
\draw[blue,
      decoration={moveto, post=lineto, post length={\dimexpr4cm+1cm}}, decorate] 
      (0,-2) -- node{4cm+1cm} (5,-2);
\draw[orange,
      decoration={moveto, post=lineto, post length={\dimexpr4cm-1cm}}, decorate] 
      (0,-3) --node{4cm-1cm} (5,-3);
    \end{tikzpicture}
\end{document}

Answer 2

The reason is basically the same as Enforcing Order of Operations on Dimension Expressions? just on an internal level of TikZ.

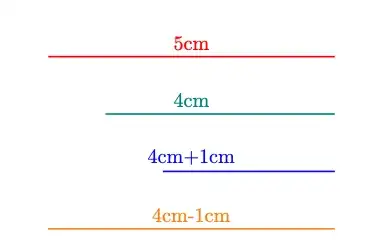
The value, for example 4cm-1cm, simply gets stored in the key /pgf/decoration/post length. Somewhere in the decoration code it is retrieved via \pgfkeysvalueof{/pgf/decoration/post length} and this is just a “dumb” replacement.

Somewhere in the code of the decoration the expression

\pgfmetadecoratedremainingdistance-\pgfkeysvalueof{/pgf/decoration/post length}

will be calculated which is

<some value>-4cm-1cm

which mathematically is the same as

<some value>-5cm

and not

<some value>-(4cm-1cm)

---

I'd argue that is somewhat of a bug in TikZ.
Similar things happen with the delta angle whose value is just subtracted from the end angle (when no start angle is given, of course). (See for example another answer of mine where I'm using () around the ternary operator because that was doing very weird things.)

---

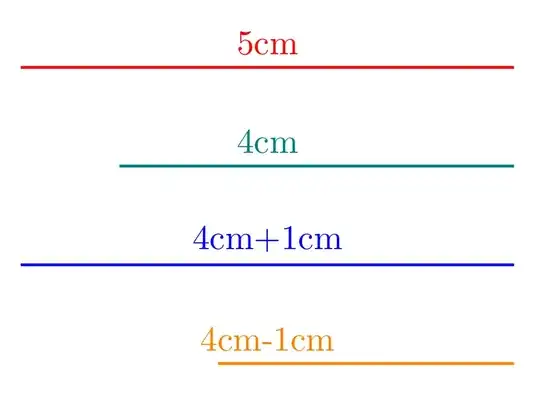
So you will need parentheses (the {} braces get stripped by PGFKeys)

\draw[blue,
decoration={moveto, post=lineto, post length=(4cm+1cm)}, decorate
] (0,-2) --node{4cm+1cm} (5,-2);
\draw[orange,
decoration={moveto, post=lineto, post length=(4cm-1cm)}, decorate
] (0,-3) --node{4cm-1cm} (5,-3);

or evaluate the result before the decoration code gets to it:

\draw[blue,
decoration={moveto, post=lineto, post length/.evaluated=4cm+1cm}, decorate
] (0,-2) --node{4cm+1cm} (5,-2);
\draw[orange,
decoration={moveto, post=lineto, post length/.evaluated=4cm-1cm}, decorate
] (0,-3) --node{4cm-1cm} (5,-3);

Technically, this will store a result without units in the key but this will get converted to pt again by PGFMath.

Of course, you can just do

\pgfmathset(length)macro\<something>{4cm±1cm}

and then use \<something> instead.

(A \dimexpr gets handed off to eTeX when PGFMath gets to it and since that is greedy it grabs as much as it can get.)

Answer 3

The plus sign isn't working either.

One way to achieve this is for e.g. by declaring a counter then either setting its value or adding and subbing numbers to/from it.

Here is your code with this implementation.

Every time I need the value of the counter I call \the<name of counter>, in this case it is named l.

\documentclass[tikz, border=1cm]{standalone}
\usetikzlibrary{decorations.pathmorphing}
\usetikzlibrary{math}
\begin{document}
    \begin{tikzpicture}[thick, above]
\newcounter{l}
\setcounter{l}{5}
\draw[red] (0,0) --node{5cm} (5,0);


\draw[teal,
decoration={moveto, post=lineto, post length=4 cm}, decorate
] (0,-1) --node{4cm} (5,-1);



\addtocounter{l}{-1}
\draw[blue,
decoration={moveto, post=lineto, post length={\thel cm}}, decorate
] (0,-2) --node{4cm+1cm} (5,-2);
\addtocounter{l}{-1}
\draw[orange,
decoration={moveto, post=lineto, post length={\thel cm}}, decorate
 ] (0,-3) --node{4cm-1cm} (5,-3);
\end{tikzpicture}

\end{document}