How to draw any polygram using tikz?

Question

I've been trying to create a command to generalize this but I don't know what I'm doing wrong. Maybe it's more complex than I thought. How should I do it? Please include descriptions to steps because I don't know too much about latex and tikz. Also explain what I'm doing wrong please.

\documentclass[parskip]{scrartcl}
\usepackage[margin=15mm]{geometry}
\usepackage{tikz}
\begin{document}
\newcommand{\polygram}[4]{%radius, number of total points, connect points skipping this number of points, draw options
\draw[#4] ({360/#2}:#1) %draw at starting point
\foreach \x in {1, ..., #2} %cycle through other points, drawing to the next, skipping #3 points
{ -- ({360/(\x+#3)}:#1)} -- cycle;
}
\tikz \polygram{2}{5}{2}{blue};
\end{document}

More info: Polygram (Wikipedia)

Answer 1

I think, what you're after is something like this:

\documentclass[tikz, border=1cm]{standalone}
\begin{document}
\newcommand{\polygram}[4][]{
    % options, radius, # of total points, # of skipping points
    \draw[#1] (0:#2) 
    \foreach \x in {1,...,#3} {
        -- ({360/#3(\x-1)#4}:#2) 
    } -- cycle
}
\tikz \polygram[blue]{2}{5}{2};
\end{document}

As comparison, \tikz \polygram[blue]{2}{10}{3}; yields:

---

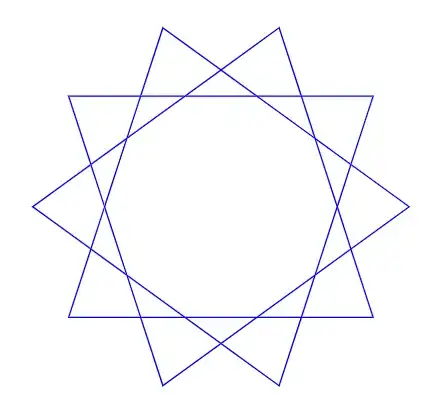
Note that 0 degees is to the right. In order to draw the diagram with its starting point upwards, you need to turn everything by 90 degrees counterclockwise:

\documentclass[tikz, border=1cm]{standalone}
\begin{document}
\newcommand{\polygram}[4][]{
    % options, radius, # of total points, # of skipping points
    \draw[#1] (90:#2) 
    \foreach \x in {1,...,#3} {
        -- ({360/#3(\x-1)#4+90}:#2) 
    } -- cycle
}
\tikz \polygram[blue]{2}{5}{2};
\end{document}

---

And because I recently got to like pics so much, a solution using a pic:

\documentclass[tikz, border=1cm]{standalone}
\begin{document}
\tikzset{
    pics/polygram/.style={
        code={
            \tikzset{polygram/.cd, #1}
            \draw[pic actions] (90:{\pgfkeysvalueof{/tikz/polygram/radius}}) 
                \foreach \x in {1,...,{\pgfkeysvalueof{/tikz/polygram/total points}}} {
                    -- ({ 360 /
                          \pgfkeysvalueof{/tikz/polygram/total points} *
                          (\x - 1) * 
                          \pgfkeysvalueof{/tikz/polygram/skipping points} + 
                          90 } : 
                        {\pgfkeysvalueof{/tikz/polygram/radius}}) 
                } -- cycle;

        }
    },
    polygram/.cd,
    radius/.initial=1,
    total points/.initial=5,
    skipping points/.initial=2,
}
\tikz \pic[blue] {polygram={radius=2}};
\tikz \pic[red, thick] {polygram={total points=7}};
\tikz \pic[cyan, dashed] {polygram={radius=2, total points=7, skipping points=3}};
\end{document}

---

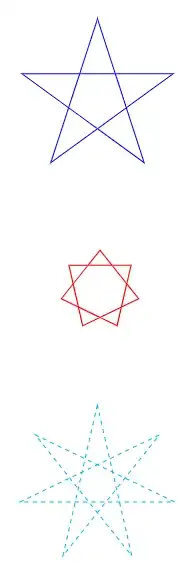
This version also works with p (total number of points) and q (number of points skipped) that are evenly divisible:

\documentclass[tikz, border=1cm]{standalone}
\begin{document}
\tikzset{
    pics/polygram/.style={
        code={
            \tikzset{polygram/.cd, #1}
            \pgfmathparse{
                mod(
                    \pgfkeysvalueof{/tikz/polygram/total points} ,
                    \pgfkeysvalueof{/tikz/polygram/skipping points} 
                ) == 0 ? \pgfkeysvalueof{/tikz/polygram/skipping points} : 1
            }
            \foreach \r in {0,...,\pgfmathresult} {
                \begin{scope}[rotate={360/\pgfkeysvalueof{/tikz/polygram/total points}\r}]
                    \draw[pic actions] (90:{\pgfkeysvalueof{/tikz/polygram/radius}}) 
                        \foreach \x in {1,...,{\pgfkeysvalueof{/tikz/polygram/total points}}} {
                            -- ({ 360 /
                                  \pgfkeysvalueof{/tikz/polygram/total points} 
                                  (\x - 1) * 
                                  \pgfkeysvalueof{/tikz/polygram/skipping points} + 
                                  90 } : 
                                {\pgfkeysvalueof{/tikz/polygram/radius}}) 
                        } -- cycle;
                \end{scope}
            }
        }
    },
    polygram/.cd,
    radius/.initial=1,
    total points/.initial=5,
    skipping points/.initial=2,
}
\tikz \pic[blue] {polygram={total points=12, skipping points=4}};
\tikz \pic[blue] {polygram={total points=6, skipping points=2}};
\end{document}

---

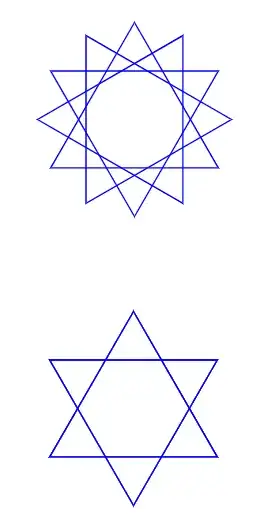
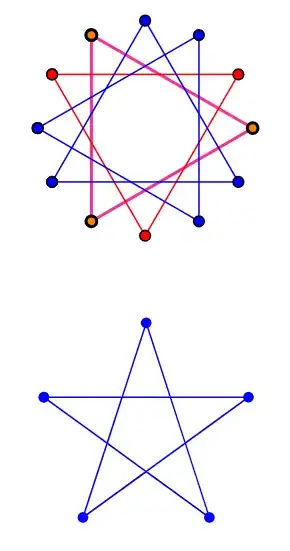
An adjustment to be able to style the different layers individually and to add stylable dots at the tips:

\documentclass[tikz, border=1cm]{standalone}
\begin{document}
\tikzset{
    pics/polygram/.style={
        code={
            \tikzset{polygram/.cd, #1}
            \pgfmathsetmacro{\polygramlayers}{
                mod(
                    \pgfkeysvalueof{/tikz/polygram/total points} ,
                    \pgfkeysvalueof{/tikz/polygram/skipping points} 
                ) == 0 ? \pgfkeysvalueof{/tikz/polygram/skipping points} : 1
            }
            \pgfmathsetmacro{\polygramnodesperlayer}{
                int(
                    \pgfkeysvalueof{/tikz/polygram/total points} / 
                    \polygramlayers 
                )
            }
            \foreach \r in {1,...,\polygramlayers} {
                \tikzset{polygram layer \r/.initial={}}
                \begin{scope}[
                    rotate={360/\pgfkeysvalueof{/tikz/polygram/total points}\r}, 
                    pic actions,
                    polygram layer \r
                ]
                    \draw (90:{\pgfkeysvalueof{/tikz/polygram/radius}}) 
                            node[polygram dot] {}

                        \foreach \x in {1,...,\polygramnodesperlayer} {
                            -- ({ 360 /
                                  \pgfkeysvalueof{/tikz/polygram/total points} 
                                  (\x - 1) * 
                                  \pgfkeysvalueof{/tikz/polygram/skipping points} + 
                                  90 } : 
                                {\pgfkeysvalueof{/tikz/polygram/radius}}) 
                                    node[polygram dot] {}
                        } -- cycle;
                \end{scope}
            }
        }
    },
    polygram dot/.style={circle, fill, inner sep=1pt},
    polygram/.cd,
    radius/.initial=1,
    total points/.initial=5,
    skipping points/.initial=2,
}
\tikz 
    \pic[blue, 
        polygram dot/.append style={draw=black},
        polygram layer 1/.style={magenta, thick, polygram dot/.append style={fill=orange}}, 
        polygram layer 2/.style={red}
    ] 
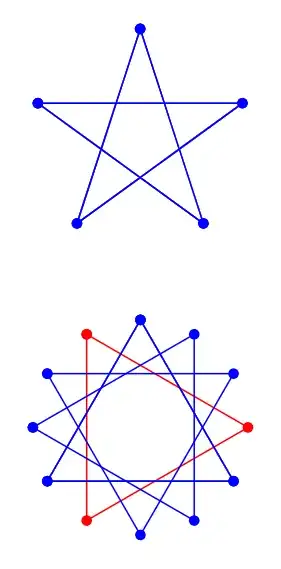
    {polygram={total points=12, skipping points=4}};
\tikz 
    \pic[blue] {polygram={total points=5, skipping points=3}};
\end{document}

---

A non-pic version of the last variant would be:

\documentclass[tikz, border=1cm]{standalone}
\begin{document}
\tikzset{
    polygram dot/.style={circle, fill, inner sep=1pt}
}
\newcommand{\polygram}[4][]{
    % options, radius, # of total points, # of skipping points
    \pgfmathsetmacro{\polygramlayers}{
        mod(#3,#4) == 0 ? #4 : 1
    }
    \pgfmathsetmacro{\polygramnodesperlayer}{
        int(#3/\polygramlayers)
    }
    \node at (0,0) {\polygramlayers};
    \foreach \r in {0,...,\polygramlayers} {
        \tikzset{polygram layer \r/.initial={}}
        \begin{scope}[rotate={360/#3 * \r}, #1, polygram layer \r]
            \draw (90:{#2}) node[polygram dot] {}

                \foreach \x in {1,...,\polygramnodesperlayer} {
                    -- ({360/#3 * (\x - 1) * #4 + 90}:{#2}) node[polygram dot] {}
                } -- cycle;
        \end{scope}
    }
}
\tikz \polygram[blue]{1}{5}{2};
\tikz \polygram[blue, polygram layer 1/.style={red}]{1}{12}{4};
\end{document}

Answer 2

This defines one key Schlaefli star = p/q (where p and q are integers that do not share any factors). This corresponds to the section Generalized regular polygons on your linked Wikipedia page.

This key is also used internally by Schlaefli comp = n/m which follows the section Regular compound polygons. Again, n and m must be integers.
Choosing n and m so that they fulfill the conditions of p and q will lead to a GCD of 1 and a “normal” star will be drawn, just as an edge.

---

Both will only work for integers. Technically, not all the \pgfintevals are necessary (they carry out integer arithmetics via eTeX' primitives) but they together with .expanded lower the need to evaluate the same expression multiple times.

If you need to change the radius, use scale or change the x and y value of the xyz coordinate system. The transformation rotate can be used to rotate the whole polygram.

---

I've chose not to define a command that issues \draw itself but to implement this as a key. This means, the control is with you with the actual \draw. You can also use \fill or other options without an extra interface.

The compound polygons are implemented via an edge which means they can each have a different color or other options. (You could draw one, fill the other and pattern the third …) This is controlled via the Schlaefli edge key that takes two arguments, the current edge and the total number of edges. Though, they go from 0 to k−1 instead of 1 to k.

Similar, the Schlaefli dot key gets the number of the corner (counting from 0) forwarded which can be used as #1.

So with something like

\tikz[
  scale=2,
  ultra thick,
  Schlaefli edge/.style 2 args={
    draw=c#1,
    Schlaefli dot/.append style={thick, minimum size=2mm, fill=c#1, draw=c##1}},
  color let/.code args={#1=#2}{\colorlet{c#1}{#2}},
  color let/.list={
    0=red, 1=orange, 2=yellow, 3=green, 4=blue, 5=violet, 6=magenta}
] \path[Schlaefli comp=28/7];

you can produce this, uh, beautiful picture:

---

I'm using the full arc key and the R post-fix operator of the ext.misc library of my tikz-ext package since it allows me to not have to calculate the angular steps myself. Simply giving the options full arc = 5 means that 1R equals 72°, 2R equals 144° and so one. This is of course not necessary and in fact, in Schlaefli comp I've used the explicit version to rotate each of the k polygons.

Code

\documentclass[tikz]{standalone}
\usetikzlibrary{ext.misc}
\tikzset{
  Schlaefli dot/.style={
    shape=circle, inner sep=+0pt, fill, minimum size=+2.5pt, node contents=},
  Schlaefli star/.style args={#1/#2}{
    full arc={#1},
    insert path={
      (0R:1 and 1) node[Schlaefli dot=0]
        foreach \CORNER in {1,...,\pgfinteval{#1-1}}{
        -- ({\CORNER*(#2)*1R}:1 and 1) node[Schlaefli dot/.expanded=\CORNER]}
        -- cycle}},
  Schlaefli comp/.style args={#1/#2}{
    /utils/exec=\pgfmathgcd{#1}{#2}\let\tikzSchlaefliGCD\pgfmathresult,
    insert path={
     foreach[expand list] \POLY in {0, ..., \pgfinteval{\tikzSchlaefliGCD-1}}{
       (0,0) edge[
         Schlaefli edge/.try/.expanded={\POLY}{\pgfinteval{\tikzSchlaefliGCD-1}},
         to path/.expanded={[rotate=\pgfinteval{360/(#1)*\POLY},
           Schlaefli star=\pgfinteval{(#1)/\tikzSchlaefliGCD}/%
                          \pgfinteval{(#2)/\tikzSchlaefliGCD}]}]()}}}}
\begin{document}
\tikz[
  thick, line join=round,
  Schlaefli edge/.style 2 args={
    color/.pgfmath wrap={red!##1!orange}{#1/#2*100}},
  row sep=1mm, column sep=1mm]
\matrix{
  \draw[Schlaefli star= 5/2];
& \draw[Schlaefli star= 7/2];
& \draw[Schlaefli star= 7/3];
& \draw[Schlaefli star= 8/3]; \\
% https://en.wikipedia.org/wiki/Heptagram#/media/File:Heptagrams.svg
  \tikzset{Schlaefli dot/.append style=coordinate, rotate=90}
  \draw[red,   Schlaefli star=7/1];
  \draw[blue,  Schlaefli star=7/2];
  \draw[green, Schlaefli star=7/3];
& \draw[Schlaefli star= 9/2];
& \draw[Schlaefli star= 9/4];
& \draw[Schlaefli star=10/3]; \\
  \path[Schlaefli comp= 6/2];
& \path[Schlaefli comp= 9/3];
& \path[Schlaefli comp=12/4];
& \path[Schlaefli comp= 8/2]; \\
  \path[Schlaefli comp=12/3];
& \path[Schlaefli comp=10/2];
& \path[Schlaefli comp=10/4];
& \path[
    c0/.style=red, c1/.style=green, c2/.style=orange,
    c3/.style=blue, c4/.style=yellow!50!black,
    Schlaefli edge/.append style=c##1,
    Schlaefli dot/.append style=black,
    Schlaefli comp=15/6];
\\};
\tikz[
  scale=2,
  ultra thick,
  Schlaefli edge/.style 2 args={
    draw=c#1,
    Schlaefli dot/.append style={thick, minimum size=2mm, fill=c#1, draw=c##1},
  },
  color let/.code args={#1=#2}{\colorlet{c#1}{#2}},
  color let/.list={
    0=red, 1=orange, 2=yellow, 3=green, 4=blue, 5=violet, 6=magenta}
] \path[Schlaefli comp=28/7];
\begin{tikzpicture}[Schlaefli dot/.append style=coordinate, rotate=90]
  \fill[red,   Schlaefli star=7/1];
  \fill[blue,  Schlaefli star=7/2];
  \fill[green, Schlaefli star=7/3];
\end{tikzpicture}
\end{document}

Output

Answer 3

This creates a polygram with \nsides sides.

\documentclass[tikz,border=5]{standalone}
\def\nsides{5}
\begin{document}
    \begin{tikzpicture}[declare function={r=2;c=360/\nsides;}]
        \foreach \i in {1,...,\nsides}{
            \drawblue--(\ic+2c:r);
            \fillredcircle(.03);
        }
    \end{tikzpicture}
\end{document}