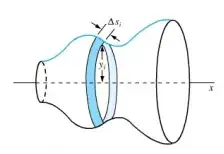
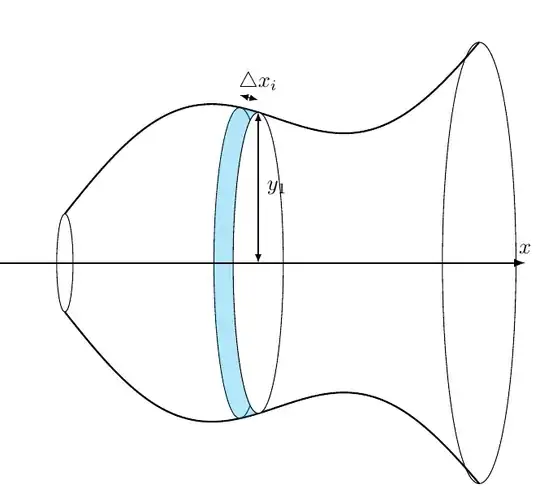
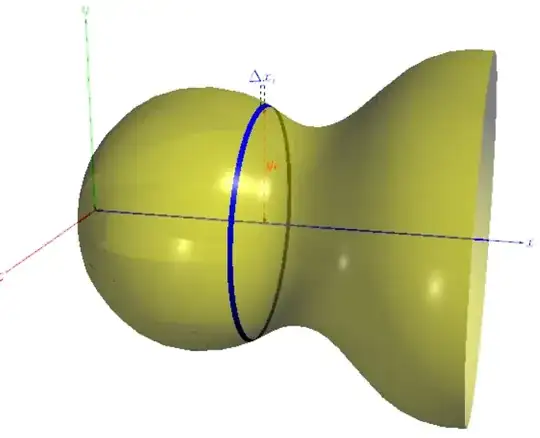
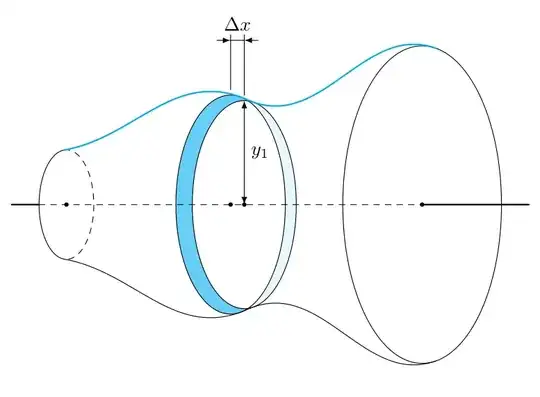
first of all I want to create this image:
Here is my MWE:
\documentclass[12pt]{article}
\usepackage{tikz}
\begin{document}
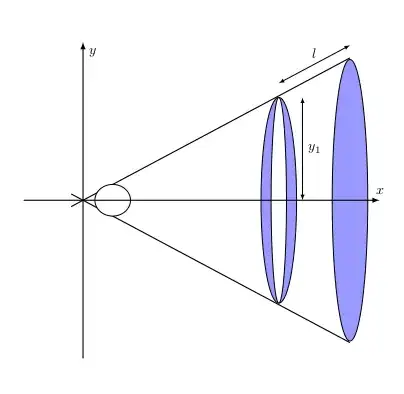
\begin{tikzpicture}[scale=1,>=latex,x=1.5cm,y=0.8cm]
\fill[fill=white,opacity=0.5] (1,0) -- plot[domain=1:4] (\x,{sqrt(2*(\x)+1))}) -- (4,0);
\fill[fill=white,opacity=0.5] (1,0) -- plot[domain=1:4] (\x,{-sqrt(2*(\x)+1))}) -- (4,0);
\draw[-,thick,domain=-.2:4.5,samples=100] plot (\x,\x) node[right] {\footnotesize $$};
\draw[-,thick,domain=-.2:4.5,samples=100] plot (\x,-\x);
% Circle
\draw[fill=white!40] (0.5,0) circle [x radius =.3 , y radius =0.5];
\draw[fill=blue!40] (3.3,0) circle [x radius =.3 , y radius =3.249489743];
\draw[fill=white!20] (3.3,0) circle [x radius =.13 , y radius =3.249489743];
\draw[fill=blue!40] (4.5,0) circle [x radius =.3 , y radius =4.449489743];
\draw[<->] (3.3,3.7) -- (4.5,4.9) node[above, midway] {\footnotesize $l$};
\draw[<->] (3.7,0) -- (3.7,3.249489743) node[right, midway] {\footnotesize $y_{1}$};
\draw[->,thick] (-1,0) -- (5,0) node[above] {\footnotesize $x$};
\draw[->,thick] (0,-5) -- (0,5) node[below right]{\footnotesize $y$};
\end{tikzpicture}
\end{document}
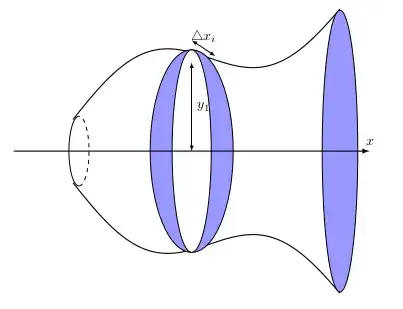
I want to create the trigonometric curves, I think it is sin2x + cos^2 x or something.. Instead of just a line y=x and y=-x that will create a cone.
Is my trick to create two circles for the middle part good enough? Is there a better method to create the middle part with two circle and white in the middle?
\draw[-,thick,domain=-55:50,samples=100] plot (\x,{sin(2*\x)+(cos(\x))^2});but the function you gave isn't the one you need https://www.desmos.com/calculator/0i2onunbmz. check the doc for tizk plot https://tikz.dev/tikz-plots – anis Jan 11 '23 at 13:14\draw[-,thick,domain=0:5,samples=10] plot (\x,{sin(2*\x)});or your suggestion, it is only a straight line. Is it the canvas size problem? – Freya the Goddess Jan 11 '23 at 13:31x + 2 cos xwith Julia it shows a curve that I want, but with tikz this line\draw[-,thick,domain=0:10,samples=10] plot (\x,{(\x) + 2*(cos(\x)) });gives straight line... what is wrong with this? – Freya the Goddess Jan 11 '23 at 13:38A sin (2 pi f t+ phi). A is the amplitude, pi is 3.14.. f is the frequency, t is time (x in the case of a plot) and phi is the phase at the origin. – anis Jan 11 '23 at 13:40\draw[-,thick,domain=0:5,samples=100] plot (\x,{sin(25*2*3.14*\x)-(cos(25*2*3.14*\x))^2-\x});i also added/subbedxto have the sin wave rise/lower. – anis Jan 11 '23 at 13:42