I am actually struggling to draw a custom neural network diagram which I had made using MS PowerPoint. I got a lot of help from my previous question but still I am not able to resolve some of the issues, in order to make the copy of the figure which I have.
Expected:
Currently, I am able to resolve the problem till this level. Here is my attempt. But there are the following error:
- How to add dots for hidden layers (showing the several hidden layers in between)
- How to make the output node to only 1 and also changing its label to summation (symbol),
Current:
\documentclass[border=3pt,tikz]{standalone}
\usepackage{tikz}
\usepackage{etoolbox} % for \ifnumcomp
\usepackage{listofitems} % for \readlist to create arrays
\tikzset{>=latex} % for LaTeX arrow head
\colorlet{mywhite}{white!80!black}
\colorlet{myred}{red!80!black}
\colorlet{myblue}{blue!80!black}
\colorlet{mygreen}{green!60!black}
\colorlet{mydarkred}{myred!40!black}
\colorlet{mydarkblue}{myblue!40!black}
\colorlet{mydarkgreen}{mygreen!40!black}
\tikzstyle{node}=[very thick,circle,draw=myblue,minimum size=22,inner sep=0.5,outer sep=0.6]
\tikzstyle{connect}=[->,thick,mydarkblue,shorten >=1]
\tikzset{ % node styles, numbered for easy mapping with \nstyle
node 1/.style={node,mydarkgreen,draw=mywhite,fill=mywhite!25},
node 2/.style={node,mydarkblue,draw=mywhite,fill=mywhite!20},
node 3/.style={node,mydarkred,draw=mywhite,fill=mywhite!20},
}
\def\nstyle{int(\lay<\Nnodlen?min(2,\lay):3)} % map layer number onto 1, 2, or 3
\begin{document}
% NEURAL NETWORK
\begin{tikzpicture}[x=2.4cm,y=1.2cm]
\readlist\Nnod{4,3,2} % array of number of nodes per layer
\readlist\Nstr{n,m,k} % array of string number of nodes per layer
\readlist\Cstr{x,h^{(\prev)},y} % array of coefficient symbol per layer
\def\yshift{0.55} % shift last node for dots
% LOOP over LAYERS
\foreachitem \N \in \Nnod{
\def\lay{\Ncnt} % alias of index of current layer
\pgfmathsetmacro\prev{int(\Ncnt-1)} % number of previous layer
\foreach \i [evaluate={\c=int(\i==\N); \y=\N/2-\i-\c*\yshift;
\x=\lay; \n=\nstyle;
\index=(\i<\N?int(\i):"\Nstr[\n]");}] in {1,...,\N}{ % loop over nodes
% NODES
\node[node \n] (N\lay-\i) at (\x,\y) {$\strut\Cstr[\n]_{\index}$};
% CONNECTIONS
\ifnumcomp{\lay}{>}{1}{ % connect to previous layer
\foreach \j in {1,...,\Nnod[\prev]}{ % loop over nodes in previous layer
\draw[white,line width=1.2,shorten >=1] (N\prev-\j) -- (N\lay-\i);
\draw[connect] (N\prev-\j) -- (N\lay-\i);
}
\ifnum \lay=\Nnodlen
\draw[connect] (N\lay-\i) --++ (0.5,0); % arrows out
\fi
}{
\draw[connect] (0.5,\y) -- (N\lay-\i); % arrows in
}
}
\path (N\lay-\N) --++ (0,1+\yshift) node[midway,scale=1.6] {$\vdots$}; % dots
}
% LABELS
\node[above=3,align=center,mydarkgreen] at (N1-1.90) {Input\[-0.2em]layer};
\node[above=2,align=center,mydarkblue] at (N2-1.90) {Hidden\[-0.2em]layers};
\node[above=3,align=center,mydarkred] at (N\Nnodlen-1.90) {Output\[-0.2em]layer};
\begin{scope}[scale=0.75,xshift=18cm,yshift=-2cm] % <---- HERE
\draw[blue!50!black] plot[domain={-1.5:5}] (\x,{sin(\x^2 r)});
\draw[blue!50!black, densely dotted] (-2,0) -- (5,0);
\draw[black, densely dashed] (0,0)
-- ++(0,-2) node[below] {$x_1$} coordinate[pos=0] (A);
\draw[black, densely dashed] (0.5,0)
-- ++(0,-2) node[below] {$x_2$} coordinate[pos=0] (B);
\draw[black, densely dashed] (1.0,0)
-- ++(0,-2) node[below] {$x_2$} coordinate[pos=0] (B);
\draw[black, densely dashed] (1.5,0)
-- ++(0,-2) node[below] {$x_2$} coordinate[pos=0] (B);
\draw[black, densely dashed] (2.0,0)
-- ++(0,-2) node[below] {$x_2$} coordinate[pos=0] (B);
\draw[thick, <->] (-2,4)
-- node[left, midway, anchor=south, rotate=90, font=\bfseries] (Y) {$f(x)$} (-2,-2)
-- node[below, pos=1, font=\bfseries] {Quad. points} (5,-2);
\end{scope}
\end{tikzpicture}
\end{document}
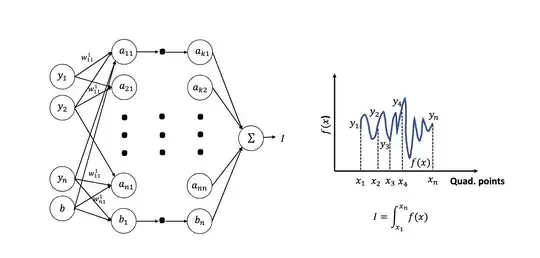
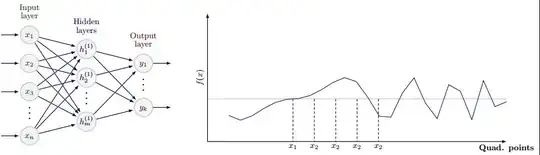
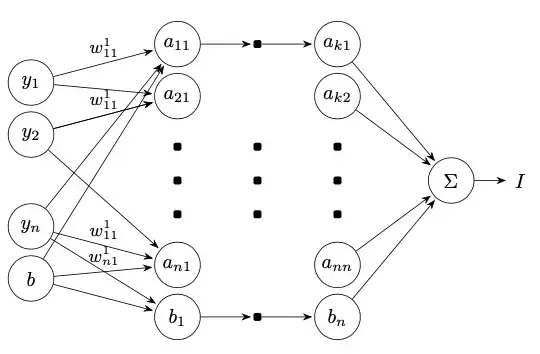
\readlist\Nnod{4,3,3,1}) or if you are not experienced with tikz maybe it would be better to start from scratch with your own code. Since the code was written for a specific case, it might be more difficult to adapt it, than to create a new less automated code where you could easily implement your wishes, e.g. setting the last node to{$\Sigma$}. – dexteritas Jan 21 '23 at 10:56