How to draw an an elliptic curve such as Y^2 = X^3 - X with tikz?

Question

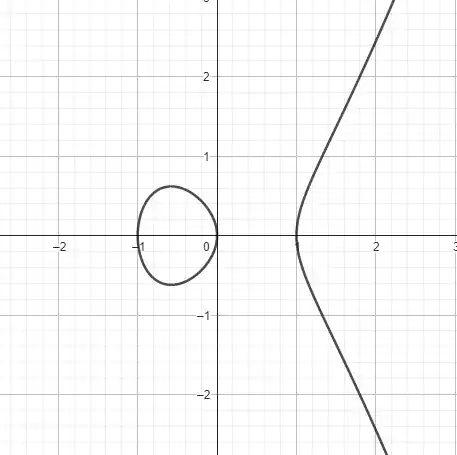
I need to draw the elliptic curve Y^2 = X^3 - X (as below) with the tikz package. As tikz doesn't support implicit curves I tried to create a pfgplot where I add a plot for the positive square roots and one for the negative square roots but I'm still experiencing problems.

This is my Code so far:

\documentclass[10pt]{article}
\usepackage{pgfplots}
\begin{document}
    \begin{tikzpicture}
        \begin{axis}[
            axis x line=center,
            axis y line=center,
            xtick={-1,1},
            xmin=-2,
            xmax=2,
            ymin=-2,
            ymax=2,
            ]
            \addplot[mark=none,samples=200,domain=-2:2] {sqrt(x^3-x)};
            \addplot[mark=none,samples=200,domain=-2:2] {-sqrt(x^3-x)};
        \end{axis}
    \end{tikzpicture}
\end{document}

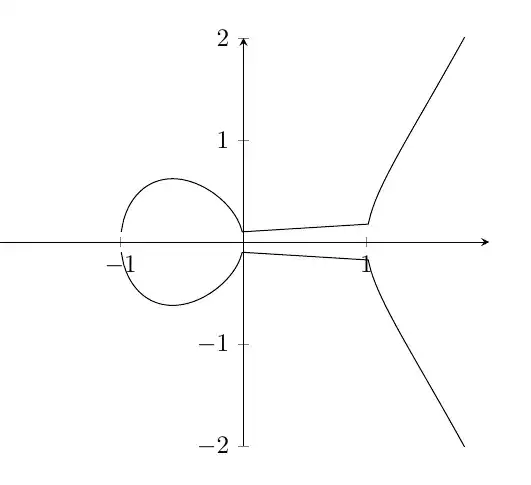
Which produces this output:

As you see, the curve is not connected near the x-Axis and there are also weird lines between 0 and 1. Is there a way to fix these problems or is there a better way to plot the ellipse all together?

Answer 1

You can make a reparametrization of the curve or simpler set your samples to an odd number. Setting your samples to an odd number will in this case sample the curve at the critical points, x=-1, x=0 and x=1. The only thing left is to make sure that the two sides are not connected by a line - this can be done by splitting the domain on two plots or with a filter like this:

\documentclass[tikz, border=1cm]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.18}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
axis lines=center,
xtick={-1,1},
xmin=-2, xmax=2,
ymin=-2, ymax=2,
]
\addplot[red, domain=-2:2, samples=201, y filter/.expression={x>0&&x<1?nan:y}, unbounded coords=jump, smooth] {sqrt(x^3-x)};
\addplot[red, domain=-2:2, samples=201, y filter/.expression={x>0&&x<1?nan:y}, unbounded coords=jump, smooth] {-sqrt(x^3-x)};
\end{axis}
\end{tikzpicture}
\end{document}