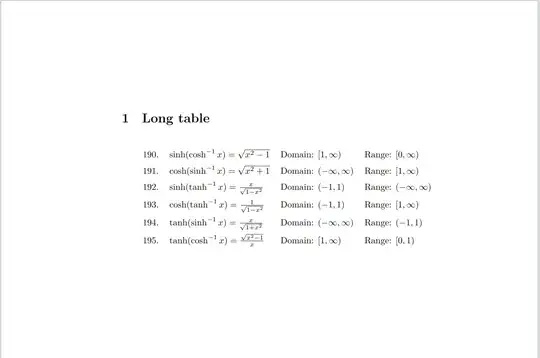
My code excluding preamble (don't judge please):
\subsection{Inverse Hyperbolic Trigonometric Identities}
\raggedright\setlength{\parindent}{45pt}
\begin{enumerate}[align=left,widest=a,labelindent=16mm,leftmargin=!]
\incrvariable\x
\setcounter{enumi}{\x}
\item%194
$
\begin{aligned}[t]
\sinh(\cosh^{-1}{x})=\sqrt{x^2-1} \hspace{20pt} &\text{Domain: } [1,\infty) \hspace{26.5pt} &&\text{Range: } [0,\infty)
\end{aligned}
$
\incrvariable\x
\item%195
$
\begin{aligned}[t]
\cosh(\sinh^{-1}{x})=\sqrt{x^2+1} \hspace{20pt} &\text{Domain: } (-\infty,\infty) \hspace{10pt} &&\text{Range: } [1,\infty)
\end{aligned}
$
\incrvariable\x
\item%196
$
\begin{aligned}[t]
\sinh(\tanh^{-1}{x})=\frac{x}{\sqrt{1-x^2}} \hspace{16.4pt} &\text{Domain: } (-1,1) \hspace{22pt} &&\text{Range: } (-\infty,\infty)
\end{aligned}
$
\incrvariable\x
\item%197
$
\begin{aligned}[t]
\cosh(\tanh^{-1}{x})=\frac{1}{\sqrt{1-x^2}} \hspace{15.25pt} &\text{Domain: } (-1,1) \hspace{21.9pt} &&\text{Range: } [1,\infty)
\end{aligned}
$
\incrvariable\x
\item%198
$
\begin{aligned}[t]
\tanh(\sinh^{-1}{x})=\frac{x}{\sqrt{1+x^2}} \hspace{16.72pt} &\text{Domain: } (-\infty,\infty) \hspace{9.5pt} &&\text{Range: } (-1,1)
\end{aligned}
$
\incrvariable\x
\item%199
$
\begin{aligned}[t]
\tanh(\cosh^{-1}{x})=\frac{\sqrt{x^2-1}}{x} \hspace{15.48pt} &\text{Domain: } [1,\infty) \hspace{26.1pt} &&\text{Range: } [0,1)
\end{aligned}
$
\end{enumerate}
The \hspace{} is the important (and annoying) part.
How can I improve my code without changing "enumerate" and "aligned" or something else that looks almost identical? (Something that keeps track of elapsed pts?)
OR with preamble here: (it's looonnng)
\documentclass[12pt, twoside]{article}
\usepackage[utf8]{inputenc}
\usepackage{indentfirst}
\usepackage[left=1.2in,right=1.2in,top=1in,bottom=1in]{geometry}
\usepackage{titling}
\usepackage{titlesec}
\usepackage{pgfplots}
\usepackage{tikz}
\pgfplotsset{compat=1.18, width=10cm}
\usepackage[fleqn]{amsmath}
\usepackage{amssymb}
\usepackage{mathtools}
\usepackage{newunicodechar}
\DeclareMathOperator{\sgn}{sgn}
\newunicodechar{ℤ}{\mathbb{Z}}
\newunicodechar{ℝ}{\mathbb{R}}
\usepackage{enumitem}
\usepackage{graphicx}
\setlength\mathindent{3cm}
\usepackage{etoolbox}
\usepackage{microtype}
\usepackage{array}
\usepackage{booktabs}
\usepackage{xcolor}
\usepackage{romannum}
\usepackage{tocloft} %Change font size of TOC
%\renewcommand*{\arraystretch}{1.9}
\newcommand{\ra}[1]{\renewcommand{\arraystretch}{#1}}
\newcolumntype{C}{>{$\displaystyle}c<{$}}
\renewcommand{\contentsname}{Table of Content}
\DeclareMathOperator{\sech}{sech}
\DeclareMathOperator{\csch}{csch}
\usepgfplotslibrary{fillbetween}
\AtBeginDocument{\addtocontents{toc}{\small}}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Odd page number on the right
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\def\align@preamble{%
&\hfil
\strut@
\setboxz@h{@lign$\m@th\displaystyle{##}$}%
\ifmeasuring@\savefieldlength@\fi
\llap{\set@field}%
\tabskip\z@skip
&\setboxz@h{@lign$\m@th\displaystyle{{}##}$}%
\ifmeasuring@\savefieldlength@\fi
\rlap{\set@field}
\hfil
\tabskip\alignsep@
}
\titleformat{\section}
{\normalfont\huge\bfseries}{\makebox[45pt][l]{\thesection}}{0pt}{}
\titleformat{\subsection}
{\normalfont\large\bfseries}{\makebox[45pt][l]{\thesubsection}}{0pt}{}
\titleformat{\subsubsection}
{\normalfont\normalsize\bfseries}{\makebox[45pt][l]{\thesubsubsection}}{0pt}{}
\setlength{\droptitle}{-1em}
\setlength{\parindent}{45pt}
\title{\Huge{\textbf{Mathematics Directory}}}
\author{\Large{Zhiyuan Liu}}
\date{}
%\newcommand\X{0}
%\renewcommand\X{0} %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\def\newvariable#1{\gdef#1{0}}
\def\addtovariable#1#2{\xdef#1{\number\numexpr#1+#2\relax}}
\def\incrvariable#1{\addtovariable#1{1}}
\newvariable\x
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\begin{document}
\maketitle
\section{}
\subsection{Inverse Hyperbolic Trigonometric Identities}
\raggedright\setlength{\parindent}{45pt}
\begin{enumerate}[align=left,widest=a,labelindent=16mm,leftmargin=!]
\incrvariable\x
\setcounter{enumi}{\x}
\item%194
$
\begin{aligned}[t]
\sinh(\cosh^{-1}{x})=\sqrt{x^2-1} \hspace{20pt} &\text{Domain: } [1,\infty) \hspace{26.5pt} &&\text{Range: } [0,\infty)
\end{aligned}
$
\incrvariable\x
\item%195
$
\begin{aligned}[t]
\cosh(\sinh^{-1}{x})=\sqrt{x^2+1} \hspace{20pt} &\text{Domain: } (-\infty,\infty) \hspace{10pt} &&\text{Range: } [1,\infty)
\end{aligned}
$
\incrvariable\x
\item%196
$
\begin{aligned}[t]
\sinh(\tanh^{-1}{x})=\frac{x}{\sqrt{1-x^2}} \hspace{16.4pt} &\text{Domain: } (-1,1) \hspace{22pt} &&\text{Range: } (-\infty,\infty)
\end{aligned}
$
\incrvariable\x
\item%197
$
\begin{aligned}[t]
\cosh(\tanh^{-1}{x})=\frac{1}{\sqrt{1-x^2}} \hspace{15.25pt} &\text{Domain: } (-1,1) \hspace{21.9pt} &&\text{Range: } [1,\infty)
\end{aligned}
$
\incrvariable\x
\item%198
$
\begin{aligned}[t]
\tanh(\sinh^{-1}{x})=\frac{x}{\sqrt{1+x^2}} \hspace{16.72pt} &\text{Domain: } (-\infty,\infty) \hspace{9.5pt} &&\text{Range: } (-1,1)
\end{aligned}
$
\incrvariable\x
\item%199
$
\begin{aligned}[t]
\tanh(\cosh^{-1}{x})=\frac{\sqrt{x^2-1}}{x} \hspace{15.48pt} &\text{Domain: } [1,\infty) \hspace{26.1pt} &&\text{Range: } [0,1)
\end{aligned}
$
\end{enumerate}
\end{document}
OR someone may have already answered it. Tell me the post. Cheers.