TeXworks editor question

Question

TeXworks editor showed error.

\documentclass{article}
\begin{document}
We can use the linearity of expectation to find \mathbb{E}[S_n]:
\begin{align*}
\mathbb{E}[S_n] &= \mathbb{E}[X_1 + X_2 + \dots + X_n] \
&= \mathbb{E}[X_1] + \mathbb{E}[X_2] + \dots + \mathbb{E}[X_n] \
&= n\mathbb{E}[X_1] \
&= n\left(\mathbb{P}{X_1=2}\cdot 2 + \mathbb{P}{X_1=-1}\cdot(-1)\right)\
&= n\left(\frac{2}{3}\cdot 2 + \frac{1}{3}\cdot(-1)\right)\
&= \frac{4n-1}{3}.
\end{align*}
To find $\mathbb{E}[S^2_n]$, we can use the fact that $\mathbb{E}[X_iX_j]=0$ for $i\neq j$ (since the $X_i$ are independent and have mean zero). We have:
\begin{align}
\mathbb{E}[S^2_n] &= \mathbb{E}[(X_1+X_2+\dots+X_n)^2] 

&= \mathbb{E}\left[\sum_{i=1}^n X_i^2 + 2\sum_{i<j}X_iX_j\right] 

&= \sum_{i=1}^n \mathbb{E}[X_i^2] + 2\sum_{i<j}\mathbb{E}[X_i]\mathbb{E}[X_j] 

&= n\mathbb{E}[X_1^2] + n(n-1)\mathbb{E}[X_1]^2 

&= n\left(\mathbb{P}{X_1=2}\cdot 2^2 + \mathbb{P}{X_1=-1}\cdot(-1)^2\right) + n(n-1)\left(\frac{4}{9}\right) 

&= \frac{10n+8n(n-1)}{9} 

&= \frac{8n^2+2n}{3}.
\end{align}
We can expand $S_n^3$ as follows:
\begin{align}
S_n^3 &= (X_1 + X_2 + \cdots + X_n)^3 

&= X_1^3 + 3X_1^2X_2 + 3X_1^2X_3 + \cdots + 3X_{n-1}^2X_n + X_2^3 + 3X_2^2X_3 + \cdots + 3X_{n-2}^2X_n + \cdots + X_n^3 

&\qquad + 3X_1X_2^2 + 3X_1X_3^2 + \cdots + 3X_1X_{n-1}^2 + 3X_2X_3^2 + \cdots + 3X_{n-2}X_n^2 + \cdots + 3X_{n-1}X_n^2 

&\qquad + 6X_1X_2X_3 + \cdots + 6X_{n-2}X_{n-1}X_n.
\end{align}
Note that each term in this expansion has an expectation of $0$, since $\mathbb{E}[X_j] = 2\cdot \frac13 - 1\cdot \frac23 = 0$ and $\mathbb{E}[X_j^2] = 2^2\cdot \frac13 + (-1)^2\cdot \frac23 = \frac43$. Therefore, we have
\begin{align}
\mathbb{E}[S_n^3] &= \sum_{j=1}^n \mathbb{E}[X_j^3] + 3 \sum_{j=1}^{n-1} \sum_{k=j+1}^n \mathbb{E}[X_jX_k^2] + 3 \sum_{j=1}^{n-2} \sum_{k=j+1}^{n-1} \sum_{\ell=k+1}^n \mathbb{E}[X_jX_kX_\ell] 

&= n\cdot \mathbb{E}[X_1^3] + 3{n \choose 2}\mathbb{E}[X_1X_2^2] + 3{n \choose 3}\mathbb{E}[X_1X_2X_3].
\end{align}
To compute these expectations, we use the given probabilities for $X_j$:
\begin{align}
\mathbb{E}[X_1^3] &= 2^3\cdot \frac13 + (-1)^3\cdot \frac23 = 0, 

\mathbb{E}[X_1X_2^2] &= 2\cdot 2^2\cdot \frac13 + (-1)\cdot 2^2\cdot \frac23 = 0, 

\mathbb{E}[X_1X_2X_3] &= 2\cdot 2\cdot \frac13 + 2\cdot (-1)\cdot \frac23 = 0.
\end{align}
Therefore, we have $\mathbb{E}[S_n^3] = 0$ for all $n$.
\end{document}

Answer 1

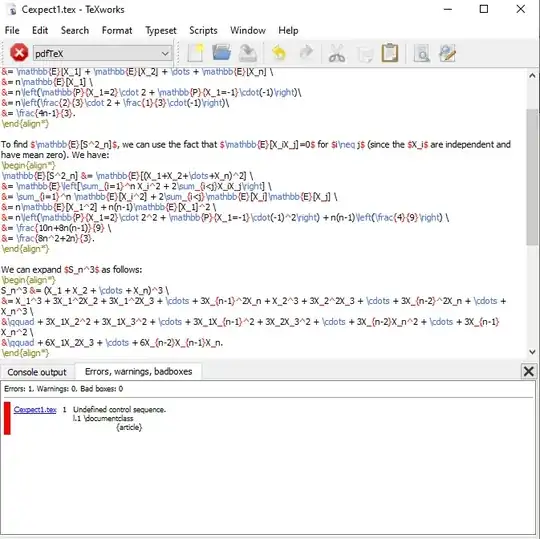
(Edit: I am only answering the pdftex/TeXworks issue as @Mico pointed out the \\ error :))

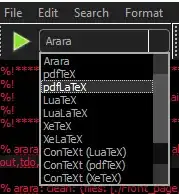
You are trying to compile with pdftex instead of pdflatex. Go to the dropdown arrow next to pdftex:

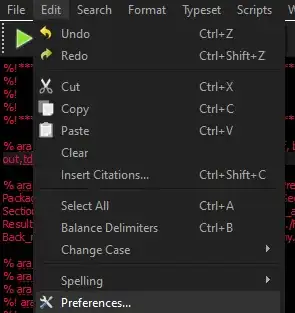
Click on pdflatex and compile. To change the default, go to Edit -> Preferences:

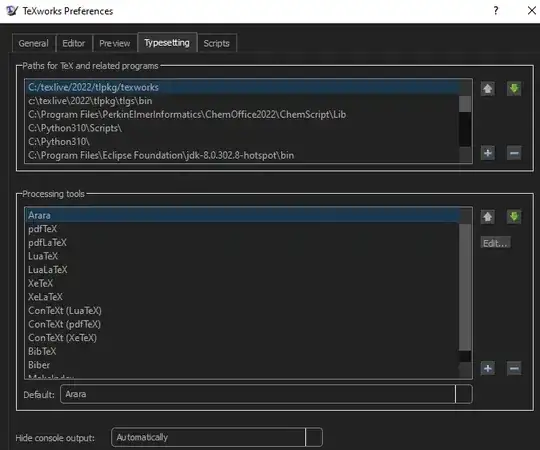
then to the Typesetting menu:

and at the very bottom, change the Default: to pdflatex (or whichever you prefer). pdftex, luatex, xetex are different to pdflatex and xelatex, lualatex (explained more thoroughly here: What's the difference between pdfTeX and pdfLaTeX?)