I am a bit desperate. I've been learning LateX for a while now. I have already looked for help in this forum but I can't adjust it to my problem.
I have a 25x25 Matrix. I have bottom lines (with Lambdas) and on the right side, there are the variables. Because the matrix is so big it does not fit on one side. I'd like to split it into a few pages. Thank you
\documentclass{article}
\usepackage{booktabs}
\usepackage{ltablex}
\begin{document}
\begin{table}
\begin{tabular}{llllllllllllllllllllllll|l}
$\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.005 \angle 156.59)}$ & $\mathbf{(0.005 \angle -156.59)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.229 \angle 3.19)}$ & $\mathbf{(0.229 \angle -3.19)}$ & $\mathbf{(0.000 \angle -11.91)}$ & $\mathbf{(0.000 \angle 11.91)}$ & $\mathbf{(0.071 \angle 21.78)}$ & $\mathbf{(0.071 \angle -21.78)}$ & $\mathbf{(0.027 \angle -180.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.002 \angle 180.00)}$ & $\mathbf{(0.087 \angle 180.00)}$ & $\mathbf{(0.355 \angle -0.00)}$ & $\mathbf{(0.513 \angle -180.00)}$ & $\mathbf{(0.272 \angle 0.00)}$ & $\mathbf{(5.376 \angle -68.74)}$ & $\mathbf{(5.376 \angle 68.74)}$ & $\mathbf{(3.475 \angle 180.00)}$ & $\Delta\delta_{G_1}$ \
$\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.005 \angle 156.59)}$ & $\mathbf{(0.005 \angle -156.59)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.229 \angle 3.20)}$ & $\mathbf{(0.229 \angle -3.20)}$ & $\mathbf{(0.000 \angle -11.91)}$ & $\mathbf{(0.000 \angle 11.91)}$ & $\mathbf{(0.071 \angle 21.79)}$ & $\mathbf{(0.071 \angle -21.79)}$ & $\mathbf{(0.027 \angle -180.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.002 \angle -180.00)}$ & $\mathbf{(0.087 \angle -180.00)}$ & $\mathbf{(0.356 \angle 0.00)}$ & $\mathbf{(0.514 \angle -180.00)}$ & $\mathbf{(0.272 \angle -0.00)}$ & $\mathbf{(5.499 \angle -61.43)}$ & $\mathbf{(5.499 \angle 61.43)}$ & $\mathbf{(4.836 \angle -180.00)}$ & $\Delta\omega_{G_1}$ \
$\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.003 \angle -176.88)}$ & $\mathbf{(0.003 \angle 176.88)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.013 \angle 73.52)}$ & $\mathbf{(0.013 \angle -73.52)}$ & $\mathbf{(0.000 \angle -26.29)}$ & $\mathbf{(0.000 \angle 26.29)}$ & $\mathbf{(0.007 \angle 89.22)}$ & $\mathbf{(0.007 \angle -89.22)}$ & $\mathbf{(0.002 \angle 0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.009 \angle 180.00)}$ & $\mathbf{(0.060 \angle -0.00)}$ & $\mathbf{(0.682 \angle 0.00)}$ & $\mathbf{(0.023 \angle -0.00)}$ & $\mathbf{(0.101 \angle 48.36)}$ & $\mathbf{(0.101 \angle -48.36)}$ & $\mathbf{(0.108 \angle 0.00)}$ & $\Delta e_q\prime_{G_1}$ \
$\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.035 \angle -178.36)}$ & $\mathbf{(0.035 \angle 178.36)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.002 \angle -0.00)}$ & $\mathbf{(0.018 \angle -180.00)}$ & $\mathbf{(0.019 \angle -180.00)}$ & $\mathbf{(0.018 \angle 167.73)}$ & $\mathbf{(0.018 \angle -167.73)}$ & $\mathbf{(0.000 \angle 128.27)}$ & $\mathbf{(0.000 \angle -128.27)}$ & $\mathbf{(0.001 \angle 141.18)}$ & $\mathbf{(0.001 \angle -141.18)}$ & $\mathbf{(0.588 \angle 0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.171 \angle -0.00)}$ & $\mathbf{(0.381 \angle 0.00)}$ & $\mathbf{(0.002 \angle 180.00)}$ & $\mathbf{(0.002 \angle -180.00)}$ & $\mathbf{(0.006 \angle 0.00)}$ & $\mathbf{(0.000 \angle -163.48)}$ & $\mathbf{(0.000 \angle 163.48)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\Delta e_d\prime_{G_1}$ \
$\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.235 \angle 7.79)}$ & $\mathbf{(0.235 \angle -7.79)}$ & $\mathbf{(0.002 \angle 0.00)}$ & $\mathbf{(0.310 \angle -0.00)}$ & $\mathbf{(0.237 \angle 0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.002 \angle -180.00)}$ & $\mathbf{(0.008 \angle -133.27)}$ & $\mathbf{(0.008 \angle 133.27)}$ & $\mathbf{(0.000 \angle 128.40)}$ & $\mathbf{(0.000 \angle -128.40)}$ & $\mathbf{(0.001 \angle -139.64)}$ & $\mathbf{(0.001 \angle 139.64)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.000 \angle 49.90)}$ & $\mathbf{(0.000 \angle -49.90)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\Delta e_q\prime\prime_{G_1}$ \
$\mathbf{(0.001 \angle -0.00)}$ & $\mathbf{(0.261 \angle 1.34)}$ & $\mathbf{(0.261 \angle -1.34)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.008 \angle 0.00)}$ & $\mathbf{(0.017 \angle -180.00)}$ & $\mathbf{(0.199 \angle -0.00)}$ & $\mathbf{(0.403 \angle -0.00)}$ & $\mathbf{(0.011 \angle -95.13)}$ & $\mathbf{(0.011 \angle 95.13)}$ & $\mathbf{(0.000 \angle -131.85)}$ & $\mathbf{(0.000 \angle 131.85)}$ & $\mathbf{(0.000 \angle -149.53)}$ & $\mathbf{(0.000 \angle 149.53)}$ & $\mathbf{(0.081 \angle 180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.016 \angle -180.00)}$ & $\mathbf{(0.015 \angle 180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.001 \angle 0.00)}$ & $\mathbf{(0.000 \angle -163.40)}$ & $\mathbf{(0.000 \angle 163.40)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\Delta e_d\prime\prime_{G_1}$ \
$\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.005 \angle 141.68)}$ & $\mathbf{(0.005 \angle -141.68)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.301 \angle -2.36)}$ & $\mathbf{(0.301 \angle 2.36)}$ & $\mathbf{(0.001 \angle 102.96)}$ & $\mathbf{(0.001 \angle -102.96)}$ & $\mathbf{(0.037 \angle 35.51)}$ & $\mathbf{(0.037 \angle -35.51)}$ & $\mathbf{(0.015 \angle -180.00)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.007 \angle 180.00)}$ & $\mathbf{(0.004 \angle 180.00)}$ & $\mathbf{(0.167 \angle -180.00)}$ & $\mathbf{(0.535 \angle -0.00)}$ & $\mathbf{(0.325 \angle 180.00)}$ & $\mathbf{(3.970 \angle -61.25)}$ & $\mathbf{(3.970 \angle 61.25)}$ & $\mathbf{(3.489 \angle 180.00)}$ & $\Delta\delta_{G_2}$ \
$\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.005 \angle 141.68)}$ & $\mathbf{(0.005 \angle -141.68)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.301 \angle -2.36)}$ & $\mathbf{(0.301 \angle 2.36)}$ & $\mathbf{(0.001 \angle 102.96)}$ & $\mathbf{(0.001 \angle -102.96)}$ & $\mathbf{(0.037 \angle 35.51)}$ & $\mathbf{(0.037 \angle -35.51)}$ & $\mathbf{(0.015 \angle 180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.007 \angle -180.00)}$ & $\mathbf{(0.004 \angle -180.00)}$ & $\mathbf{(0.167 \angle 180.00)}$ & $\mathbf{(0.535 \angle -0.00)}$ & $\mathbf{(0.325 \angle -180.00)}$ & $\mathbf{(3.970 \angle -61.25)}$ & $\mathbf{(3.970 \angle 61.25)}$ & $\mathbf{(3.489 \angle -180.00)}$ & $\Delta\omega_{G_2}$ \
$\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.004 \angle 175.57)}$ & $\mathbf{(0.004 \angle -175.57)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.014 \angle 67.49)}$ & $\mathbf{(0.014 \angle -67.49)}$ & $\mathbf{(0.000 \angle 124.93)}$ & $\mathbf{(0.000 \angle -124.93)}$ & $\mathbf{(0.008 \angle 97.76)}$ & $\mathbf{(0.008 \angle -97.76)}$ & $\mathbf{(0.003 \angle 0.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.001 \angle 0.00)}$ & $\mathbf{(0.014 \angle 180.00)}$ & $\mathbf{(0.450 \angle -0.00)}$ & $\mathbf{(0.073 \angle 180.00)}$ & $\mathbf{(0.409 \angle 0.00)}$ & $\mathbf{(0.093 \angle 42.73)}$ & $\mathbf{(0.093 \angle -42.73)}$ & $\mathbf{(0.087 \angle 0.00)}$ & $\Delta e_q\prime_{G_2}$ \
$\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.043 \angle 168.55)}$ & $\mathbf{(0.043 \angle -168.55)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.002 \angle 180.00)}$ & $\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.011 \angle -180.00)}$ & $\mathbf{(0.016 \angle 180.00)}$ & $\mathbf{(0.037 \angle 157.51)}$ & $\mathbf{(0.037 \angle -157.51)}$ & $\mathbf{(0.000 \angle -55.47)}$ & $\mathbf{(0.000 \angle 55.47)}$ & $\mathbf{(0.005 \angle 176.43)}$ & $\mathbf{(0.005 \angle -176.43)}$ & $\mathbf{(0.660 \angle -0.00)}$ & $\mathbf{(0.001 \angle -0.00)}$ & $\mathbf{(0.135 \angle -0.00)}$ & $\mathbf{(0.399 \angle 0.00)}$ & $\mathbf{(0.010 \angle 180.00)}$ & $\mathbf{(0.007 \angle -0.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle -155.09)}$ & $\mathbf{(0.000 \angle 155.09)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\Delta e_d\prime_{G_2}$ \
$\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.283 \angle 0.24)}$ & $\mathbf{(0.283 \angle -0.24)}$ & $\mathbf{(0.009 \angle 0.00)}$ & $\mathbf{(0.218 \angle -0.00)}$ & $\mathbf{(0.227 \angle 0.00)}$ & $\mathbf{(0.004 \angle 0.00)}$ & $\mathbf{(0.009 \angle 180.00)}$ & $\mathbf{(0.008 \angle -139.29)}$ & $\mathbf{(0.008 \angle 139.29)}$ & $\mathbf{(0.000 \angle -80.38)}$ & $\mathbf{(0.000 \angle 80.38)}$ & $\mathbf{(0.002 \angle -131.09)}$ & $\mathbf{(0.002 \angle 131.09)}$ & $\mathbf{(0.001 \angle -0.00)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.002 \angle -180.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.000 \angle 44.27)}$ & $\mathbf{(0.000 \angle -44.27)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\Delta e_q\prime\prime_{G_2}$ \
$\mathbf{(0.006 \angle -0.00)}$ & $\mathbf{(0.323 \angle -11.74)}$ & $\mathbf{(0.323 \angle 11.74)}$ & $\mathbf{(0.003 \angle -180.00)}$ & $\mathbf{(0.013 \angle 0.00)}$ & $\mathbf{(0.010 \angle -0.00)}$ & $\mathbf{(0.120 \angle -0.00)}$ & $\mathbf{(0.353 \angle -0.00)}$ & $\mathbf{(0.023 \angle -105.35)}$ & $\mathbf{(0.023 \angle 105.35)}$ & $\mathbf{(0.000 \angle 44.41)}$ & $\mathbf{(0.000 \angle -44.41)}$ & $\mathbf{(0.002 \angle -114.28)}$ & $\mathbf{(0.002 \angle 114.28)}$ & $\mathbf{(0.090 \angle -180.00)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.013 \angle -180.00)}$ & $\mathbf{(0.015 \angle 180.00)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.001 \angle -0.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle -155.01)}$ & $\mathbf{(0.000 \angle 155.01)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\Delta e_d\prime\prime_{G_2}$ \
$\mathbf{(0.006 \angle 180.00)}$ & $\mathbf{(0.000 \angle -140.05)}$ & $\mathbf{(0.000 \angle 140.05)}$ & $\mathbf{(0.004 \angle 180.00)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.001 \angle 19.45)}$ & $\mathbf{(0.001 \angle -19.45)}$ & $\mathbf{(0.234 \angle 2.62)}$ & $\mathbf{(0.234 \angle -2.62)}$ & $\mathbf{(0.225 \angle -9.84)}$ & $\mathbf{(0.225 \angle 9.84)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.020 \angle -180.00)}$ & $\mathbf{(0.007 \angle -0.00)}$ & $\mathbf{(0.032 \angle -0.00)}$ & $\mathbf{(0.211 \angle 0.00)}$ & $\mathbf{(0.214 \angle 180.00)}$ & $\mathbf{(0.141 \angle -180.00)}$ & $\mathbf{(5.450 \angle 115.19)}$ & $\mathbf{(5.450 \angle -115.19)}$ & $\mathbf{(4.861 \angle -0.00)}$ & $\Delta\delta_{G_3}'$ \
$\mathbf{(0.006 \angle 180.00)}$ & $\mathbf{(0.000 \angle -140.05)}$ & $\mathbf{(0.000 \angle 140.05)}$ & $\mathbf{(0.004 \angle -180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.001 \angle 19.45)}$ & $\mathbf{(0.001 \angle -19.45)}$ & $\mathbf{(0.234 \angle 2.62)}$ & $\mathbf{(0.234 \angle -2.62)}$ & $\mathbf{(0.225 \angle -9.84)}$ & $\mathbf{(0.225 \angle 9.84)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.020 \angle 180.00)}$ & $\mathbf{(0.007 \angle 0.00)}$ & $\mathbf{(0.032 \angle 0.00)}$ & $\mathbf{(0.211 \angle -0.00)}$ & $\mathbf{(0.214 \angle 180.00)}$ & $\mathbf{(0.141 \angle -180.00)}$ & $\mathbf{(5.450 \angle 115.19)}$ & $\mathbf{(5.450 \angle -115.19)}$ & $\mathbf{(4.861 \angle 0.00)}$ & $\Delta\omega_{G_3}$ \
$\mathbf{(0.001 \angle 0.00)}$ & $\mathbf{(0.000 \angle -128.67)}$ & $\mathbf{(0.000 \angle 128.67)}$ & $\mathbf{(0.008 \angle -180.00)}$ & $\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.000 \angle 91.41)}$ & $\mathbf{(0.000 \angle -91.41)}$ & $\mathbf{(0.015 \angle 72.44)}$ & $\mathbf{(0.015 \angle -72.44)}$ & $\mathbf{(0.010 \angle 72.66)}$ & $\mathbf{(0.010 \angle -72.66)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.002 \angle -0.00)}$ & $\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.005 \angle -180.00)}$ & $\mathbf{(0.059 \angle 0.00)}$ & $\mathbf{(0.293 \angle -0.00)}$ & $\mathbf{(0.296 \angle 0.00)}$ & $\mathbf{(0.253 \angle 25.79)}$ & $\mathbf{(0.253 \angle -25.79)}$ & $\mathbf{(0.107 \angle -180.00)}$ & $\Delta e_q\prime_{G_3}$ \
$\mathbf{(0.078 \angle 180.00)}$ & $\mathbf{(0.000 \angle -156.51)}$ & $\mathbf{(0.000 \angle 156.51)}$ & $\mathbf{(0.010 \angle -0.00)}$ & $\mathbf{(0.002 \angle -0.00)}$ & $\mathbf{(0.003 \angle 0.00)}$ & $\mathbf{(0.041 \angle -180.00)}$ & $\mathbf{(0.008 \angle 180.00)}$ & $\mathbf{(0.000 \angle -172.59)}$ & $\mathbf{(0.000 \angle 172.59)}$ & $\mathbf{(0.016 \angle 169.81)}$ & $\mathbf{(0.016 \angle -169.81)}$ & $\mathbf{(0.010 \angle -8.72)}$ & $\mathbf{(0.010 \angle 8.72)}$ & $\mathbf{(0.002 \angle -0.00)}$ & $\mathbf{(0.595 \angle 0.00)}$ & $\mathbf{(0.395 \angle -0.00)}$ & $\mathbf{(0.134 \angle -0.00)}$ & $\mathbf{(0.002 \angle 180.00)}$ & $\mathbf{(0.001 \angle -0.00)}$ & $\mathbf{(0.002 \angle 0.00)}$ & $\mathbf{(0.000 \angle 16.18)}$ & $\mathbf{(0.000 \angle -16.18)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\Delta e_d\prime_{G_3}$ \
$\mathbf{(0.036 \angle 180.00)}$ & $\mathbf{(0.009 \angle 56.00)}$ & $\mathbf{(0.009 \angle -56.00)}$ & $\mathbf{(0.508 \angle -0.00)}$ & $\mathbf{(0.260 \angle -0.00)}$ & $\mathbf{(0.284 \angle -0.00)}$ & $\mathbf{(0.005 \angle -180.00)}$ & $\mathbf{(0.006 \angle 180.00)}$ & $\mathbf{(0.000 \angle -115.38)}$ & $\mathbf{(0.000 \angle 115.38)}$ & $\mathbf{(0.010 \angle -132.87)}$ & $\mathbf{(0.010 \angle 132.87)}$ & $\mathbf{(0.002 \angle -156.20)}$ & $\mathbf{(0.002 \angle 156.20)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.001 \angle 27.34)}$ & $\mathbf{(0.001 \angle -27.34)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\Delta e_q\prime\prime_{G_3}$ \
$\mathbf{(0.603 \angle 0.00)}$ & $\mathbf{(0.003 \angle 23.20)}$ & $\mathbf{(0.003 \angle -23.20)}$ & $\mathbf{(0.073 \angle -180.00)}$ & $\mathbf{(0.011 \angle 180.00)}$ & $\mathbf{(0.021 \angle 180.00)}$ & $\mathbf{(0.445 \angle -0.00)}$ & $\mathbf{(0.173 \angle 0.00)}$ & $\mathbf{(0.000 \angle -75.45)}$ & $\mathbf{(0.000 \angle 75.45)}$ & $\mathbf{(0.011 \angle -90.32)}$ & $\mathbf{(0.011 \angle 90.32)}$ & $\mathbf{(0.003 \angle 60.57)}$ & $\mathbf{(0.003 \angle -60.57)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.081 \angle 180.00)}$ & $\mathbf{(0.037 \angle -180.00)}$ & $\mathbf{(0.005 \angle -180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.000 \angle 16.26)}$ & $\mathbf{(0.000 \angle -16.26)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\Delta e_d\prime\prime_{G_3}$ \
$\mathbf{(0.004 \angle 180.00)}$ & $\mathbf{(0.000 \angle -153.51)}$ & $\mathbf{(0.000 \angle 153.51)}$ & $\mathbf{(0.006 \angle 180.00)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.001 \angle 0.00)}$ & $\mathbf{(0.000 \angle -36.89)}$ & $\mathbf{(0.000 \angle 36.89)}$ & $\mathbf{(0.297 \angle -1.84)}$ & $\mathbf{(0.297 \angle 1.84)}$ & $\mathbf{(0.175 \angle -8.52)}$ & $\mathbf{(0.175 \angle 8.52)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.017 \angle 180.00)}$ & $\mathbf{(0.016 \angle -0.00)}$ & $\mathbf{(0.063 \angle -0.00)}$ & $\mathbf{(0.399 \angle 180.00)}$ & $\mathbf{(0.191 \angle 0.00)}$ & $\mathbf{(0.193 \angle -0.00)}$ & $\mathbf{(3.691 \angle 116.16)}$ & $\mathbf{(3.691 \angle -116.16)}$ & $\mathbf{(3.279 \angle -0.00)}$ & $\Delta\delta_{G_4}$ \
$\mathbf{(0.004 \angle -180.00)}$ & $\mathbf{(0.000 \angle -153.51)}$ & $\mathbf{(0.000 \angle 153.51)}$ & $\mathbf{(0.006 \angle -180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.001 \angle 0.00)}$ & $\mathbf{(0.000 \angle -36.89)}$ & $\mathbf{(0.000 \angle 36.89)}$ & $\mathbf{(0.297 \angle -1.84)}$ & $\mathbf{(0.297 \angle 1.84)}$ & $\mathbf{(0.175 \angle -8.52)}$ & $\mathbf{(0.175 \angle 8.52)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.017 \angle -180.00)}$ & $\mathbf{(0.016 \angle 0.00)}$ & $\mathbf{(0.063 \angle 0.00)}$ & $\mathbf{(0.399 \angle -180.00)}$ & $\mathbf{(0.191 \angle 0.00)}$ & $\mathbf{(0.193 \angle -0.00)}$ & $\mathbf{(3.691 \angle 116.16)}$ & $\mathbf{(3.691 \angle -116.16)}$ & $\mathbf{(3.279 \angle 0.00)}$ & $\Delta\omega_{G_4}$ \
$\mathbf{(0.001 \angle -0.00)}$ & $\mathbf{(0.000 \angle 176.56)}$ & $\mathbf{(0.000 \angle -176.56)}$ & $\mathbf{(0.009 \angle 180.00)}$ & $\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.000 \angle 0.00)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.000 \angle -21.31)}$ & $\mathbf{(0.000 \angle 21.31)}$ & $\mathbf{(0.014 \angle 66.76)}$ & $\mathbf{(0.014 \angle -66.76)}$ & $\mathbf{(0.009 \angle 73.15)}$ & $\mathbf{(0.009 \angle -73.15)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.004 \angle 0.00)}$ & $\mathbf{(0.002 \angle -180.00)}$ & $\mathbf{(0.006 \angle -180.00)}$ & $\mathbf{(0.465 \angle 0.00)}$ & $\mathbf{(0.092 \angle 0.00)}$ & $\mathbf{(0.260 \angle -0.00)}$ & $\mathbf{(0.143 \angle 25.30)}$ & $\mathbf{(0.143 \angle -25.30)}$ & $\mathbf{(0.078 \angle -180.00)}$ & $\Delta e_q\prime_{G_4}$ \
$\mathbf{(0.086 \angle -180.00)}$ & $\mathbf{(0.000 \angle -110.32)}$ & $\mathbf{(0.000 \angle 110.32)}$ & $\mathbf{(0.004 \angle 0.00)}$ & $\mathbf{(0.001 \angle 180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.033 \angle -180.00)}$ & $\mathbf{(0.007 \angle 180.00)}$ & $\mathbf{(0.000 \angle -76.09)}$ & $\mathbf{(0.000 \angle 76.09)}$ & $\mathbf{(0.038 \angle 153.11)}$ & $\mathbf{(0.038 \angle -153.11)}$ & $\mathbf{(0.014 \angle -3.66)}$ & $\mathbf{(0.014 \angle 3.66)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.640 \angle -0.00)}$ & $\mathbf{(0.372 \angle -0.00)}$ & $\mathbf{(0.152 \angle -0.00)}$ & $\mathbf{(0.012 \angle 180.00)}$ & $\mathbf{(0.004 \angle 0.00)}$ & $\mathbf{(0.006 \angle -0.00)}$ & $\mathbf{(0.000 \angle 17.67)}$ & $\mathbf{(0.000 \angle -17.67)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\Delta e_d\prime_{G_4}$ \
$\mathbf{(0.053 \angle -180.00)}$ & $\mathbf{(0.001 \angle 1.23)}$ & $\mathbf{(0.001 \angle -1.23)}$ & $\mathbf{(0.610 \angle 0.00)}$ & $\mathbf{(0.203 \angle -0.00)}$ & $\mathbf{(0.275 \angle 0.00)}$ & $\mathbf{(0.011 \angle -180.00)}$ & $\mathbf{(0.008 \angle 180.00)}$ & $\mathbf{(0.000 \angle 131.90)}$ & $\mathbf{(0.000 \angle -131.90)}$ & $\mathbf{(0.010 \angle -138.55)}$ & $\mathbf{(0.010 \angle 138.55)}$ & $\mathbf{(0.002 \angle -155.70)}$ & $\mathbf{(0.002 \angle 155.70)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.001 \angle 0.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\mathbf{(0.002 \angle 180.00)}$ & $\mathbf{(0.000 \angle 180.00)}$ & $\mathbf{(0.001 \angle -180.00)}$ & $\mathbf{(0.001 \angle 26.84)}$ & $\mathbf{(0.001 \angle -26.84)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\Delta e_q\prime\prime_{G_4}$ \
$\mathbf{(0.661 \angle -0.00)}$ & $\mathbf{(0.000 \angle 69.39)}$ & $\mathbf{(0.000 \angle -69.39)}$ & $\mathbf{(0.028 \angle 180.00)}$ & $\mathbf{(0.006 \angle 0.00)}$ & $\mathbf{(0.001 \angle 0.00)}$ & $\mathbf{(0.352 \angle -0.00)}$ & $\mathbf{(0.149 \angle 0.00)}$ & $\mathbf{(0.000 \angle 21.05)}$ & $\mathbf{(0.000 \angle -21.05)}$ & $\mathbf{(0.027 \angle -107.02)}$ & $\mathbf{(0.027 \angle 107.02)}$ & $\mathbf{(0.004 \angle 65.63)}$ & $\mathbf{(0.004 \angle -65.63)}$ & $\mathbf{(0.000 \angle -180.00)}$ & $\mathbf{(0.087 \angle -180.00)}$ & $\mathbf{(0.035 \angle -180.00)}$ & $\mathbf{(0.006 \angle -180.00)}$ & $\mathbf{(0.002 \angle 180.00)}$ & $\mathbf{(0.001 \angle 0.00)}$ & $\mathbf{(0.001 \angle -0.00)}$ & $\mathbf{(0.000 \angle 17.75)}$ & $\mathbf{(0.000 \angle -17.75)}$ & $\mathbf{(0.000 \angle -0.00)}$ & $\Delta e_d\prime\prime_{G_4}$ \
\hline
$\qquad\lambda_{0}$ &$\qquad\lambda_{1}$ &$\qquad\lambda_{2}$ &$\qquad\lambda_{3}$ &$\qquad\lambda_{4}$ &$\qquad\lambda_{5}$ &$\qquad\lambda_{6}$ &$\qquad\lambda_{7}$ &$\qquad\lambda_{8}$ &$\qquad\lambda_{9}$ &$\qquad\lambda_{10}$ &$\qquad\lambda_{11}$ &$\qquad\lambda_{12}$ &$\qquad\lambda_{13}$ &$\qquad\lambda_{14}$ &$\qquad\lambda_{15}$ &$\qquad\lambda_{16}$ &$\qquad\lambda_{17}$ &$\qquad\lambda_{18}$ &$\qquad\lambda_{19}$ &$\qquad\lambda_{20}$ &$\qquad\lambda_{21}$ &$\qquad\lambda_{22}$ &$\qquad\lambda_{23}$ & \
\end{tabular}
\label{tab:my_label}
\end{table}
\end{document}
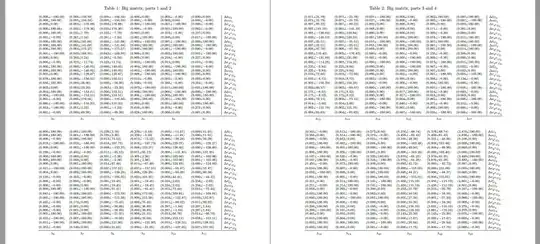
\mathbf..The font used for\mathbfis noticeably wider than the non-bold font, and the content of the last column appears to be distinctly different from what's in the other columns. Would removing the bold be possible without significantly changing the meaning? – barbara beeton Mar 13 '23 at 20:40