How to draw tangents of a function along its curve

Question

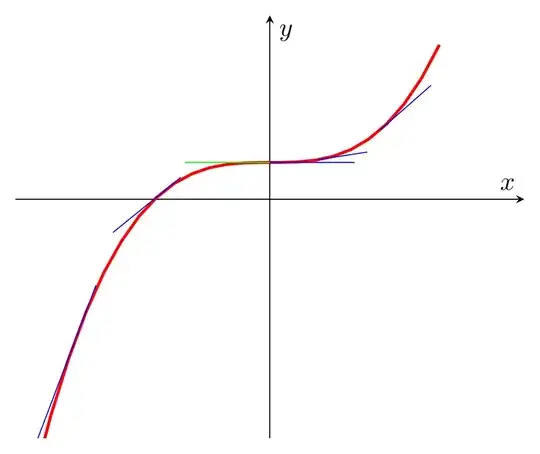
I am trying to show how the tangent is below/above the curve according to the convexity of the curve. but using the tangent equation y = f'(x0)(x-x0)+f(x0) throws the line far from the curve. so I did some testing and used the following which will not work for other functions:

\documentclass{standalone}
\standaloneconfig{border=2mm 2mm 2mm 2mm}
\usepackage{pgfplots}
\pgfplotsset{compat=newest}
\begin{document}
\begin{tikzpicture}[scale=1]
    \begin{axis}[axis lines=center,
        xlabel=$x$, ylabel=$y$,
        xtick=\empty,ytick=\empty,
        xmin=-3, xmax=3,
        ymin=-6.5, ymax=5]
       \addplot [red,thick, line width=0.4mm,domain=-3:2,unbounded coords=jump]  {0.4*x^3+1};
       \draw [->, >=Stealth,blue] (0,1) -- (1,1);
       \draw [->, >=Stealth,green] (0,1) -- (-1,1);
       \foreach \i in {0.75,1.5,...,2} {
             \addplot[domain=(\i)-0.2:(\i)+0.4, samples=100, color=blue,thin]
                 {0.4*3*(\i-0.2)^2*(x-\i+0.2)+0.4*(\i-0.2)^3+1};
                  %it should be
                  % 0.4*3*(\i)^2*(x-\i)+0.4*(\i)^3+1
                  % f'(x0)(x-x0)+f(x0)
       }
    \foreach \i in {-2.25,-1.25,...,-0.5} {
        \addplot[domain=(\i)-0.6:(\i)+0.2, samples=100, color=blue,thin]
        {0.4*3*(\i)^2*(x-\i)+0.4*(\i)^3+1};
        %same here
    }
   \end{axis}
 \end{tikzpicture}
\end{document}