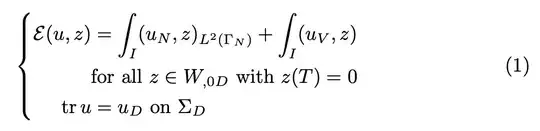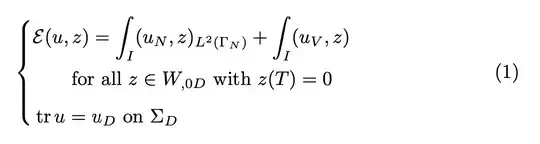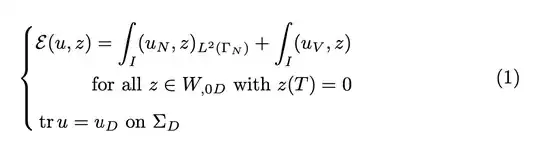Different alignments with alignat

Question

\begin{equation}\label{eq:f_formulation}
\left\{
\begin{alignedat}{3}
\E(u,z) &= \int_I(u_N,z)_{L^2(\Gamma_N)}+ \int_I(u_V,z)&\\
 &\text{for all } z \in W_{,0D} \text{ with } z(T)=0\\
\tr u &= u_D \text{ on } \Sigma_D &
\end{alignedat}
\right.
\end{equation}

An equivalent variational version is finding $u=u_0 + E u_D$, $u_0 \in W_{,0D}$ with
\begin{equation}
\left \{
\begin{alignedat}{3}\label{eq:f_formulation_variational}
\E(u_0,z) &= -\E(E u_D,z) + \int_I(u_N,z)_{L^2(\Gamma_N)}+ \int_I(u_V,z)&\\
\text{for all } z \in W_{,0D} \text{ with } z(T)=0\\
\tr u_0 &= 0 \text{ on } \Sigma_D &
\end{alignedat}
\right.
\end{equation}

Results:

I want the second equation to look as the first one, in terms of alignement: the second line's end should match up with the first line's end. With the two equals signs still being aligned. Any hint on how to achieve this?

Thanks!

The two equals signs you want to align are completely unrelated to one another, so there's no need to align them. — egreg, May 30 '23 at 21:01

score 1 · Accepted Answer · answered May 30 '23 at 21:11

You can typeset the condition as a zero width box sticking to the left.

\documentclass{article}
\usepackage{amsmath}
\newcommand{\E}{\mathcal{E}}
\DeclareMathOperator{\tr}{tr}
\begin{document}
\begin{equation}\label{eq:f_formulation}
\left{
\begin{alignedat}{2}
\E(u,z) &= \int_I(u_N,z){L^2(\Gamma_N)}+ \int_I(u_V,z)&&\
 &&&\makebox[0pt][r]{for all $z \in W{,0D}$ with $z(T)=0$}\
\tr u &= u_D \text{ on } \Sigma_D &
\end{alignedat}
\right.
\end{equation}
\end{document}

On the other hand, I see no need to look for alignment of unrelated objects.

\documentclass{article}
\usepackage{amsmath}
\newcommand{\E}{\mathcal{E}}
\DeclareMathOperator{\tr}{tr}
\begin{document}
\begin{equation}\label{eq:f_formulation}
\left{
\begin{aligned}
& \E(u,z) = \int_I(u_N,z){L^2(\Gamma_N)}+ \int_I(u_V,z) \
& \qquad\text{for all $z \in W{,0D}$ with $z(T)=0$} \[1ex]
& \tr u = u_D \text{ on } \Sigma_D
\end{aligned}
\right.
\end{equation}
\end{document}

Or, if you want that the condition is right-aligned with the top equation,

\documentclass{article}
\usepackage{amsmath}
\newcommand{\E}{\mathcal{E}}
\DeclareMathOperator{\tr}{tr}
\begin{document}
\begin{equation}\label{eq:f_formulation}
\left{
\begin{alignedat}{2}
&\E(u,z) = \int_I(u_N,z){L^2(\Gamma_N)}+ \int_I(u_V,z) \
&&\makebox[0pt][r]{for all $z \in W{,0D}$ with $z(T)=0$} \[1ex]
&\tr u = u_D \text{ on } \Sigma_D
\end{alignedat}
\right.
\end{equation}
\end{document}

Different alignments with alignat

1 Answers1