1

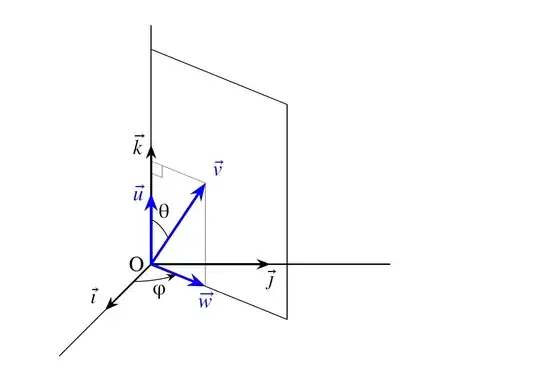
Is there a way with TikZ to calculate the cross product of two vectors?

Here is my code:

\begin{tikzpicture}[scale=2]
  \coordinate (ey) at (1,0,0);
  \coordinate (ez) at (0,1,0);
  \coordinate (ex) at (0,0,1);

\begin{scope}[x={(ex)},y={(ey)},z={(ez)}]
    \def\xM{1.2}
    \def\yM{1.6}
    \def\zM{1.8}
    \def\ech{2}

    \coordinate (O) at (0,0,0);
    \coordinate (X) at (\ech,0,0);
    \coordinate (Y) at (0,\ech,0);
    \coordinate (Z) at (0,0,\ech);
    \coordinate (Pz) at (0,0,\zM);
    \coordinate (M) at (\xM,\yM,\zM);
    \coordinate (H) at (\xM,\yM,0); 
    \coordinate (V) at ($0.4(H)+0.48(Pz)$);
    \coordinate (W) at ($0.4(H)$);
    \coordinate (Vz) at ($0.48(Pz)$);
    \coordinate (U) at ($0.33*(Pz)$);


\draw[->,thick] (0,0,0) -- (1,0,0) node[above left] {$\vec{\imath}$};
\draw[->,thick] (0,0,0) -- (0,1,0) node[below] {$\vec{\jmath}$};
\draw[->,thick] (0,0,0) -- (0,0,1) node[left] {$\vec{k}$};
  \draw (O) -- (X);
    \draw (O) -- (Y);
    \draw (O) -- (Z);
    \draw (O) -- (H);
    \draw[very thick,->,blue] (O) -- (V) node[above right] {$\vec{v}$};
    \draw[very thick,->,blue] (O) -- (W) node[below] {$\vec{w}$};
    \draw[very thick,->,blue] (O) -- (U) node[left] {$\vec{u}$};
    \draw (M) -- (H);
    \draw (M) -- (Pz);
    \draw[ultra thin] (V) -- (Vz);
    \draw[ultra thin] (V) -- (W);

    \path (O) node[left] {$O$};
    \pgfmathsetmacro\angletheta{atan(\yM/\xM)} % rotation angle for OHM plane (theta)
\draw pic [rotate around z=\angletheta,canvas is xz plane at y=0,% draws in the OHM plane
           draw,angle radius=0.75cm,
           "$\theta$",              % angle label (requires quotes library)
            angle eccentricity=1.4   % angle position
           ] {angle = V--O--Z};
\draw[ultra thin] pic [draw,angle radius=0.2cm] {right angle = V--Vz--O};
\draw pic [canvas is xy plane at z=0,% draws in the xy plane
           draw,->,angle radius=0.75cm,
           "$\varphi$",               % angle label (requires quotes library)
           angle eccentricity=1.8    % angle position
          ] {angle = X--O--H};
\end{scope}



\end{tikzpicture}

And here is the result: enter image description here

So, now I would like to draw, in plane Oxy (and with the origin O), the vector n which is the cross product u x v.

How can I do that?

projetmbc
  • 13,315
Didier
  • 1,311

1 Answers1

1

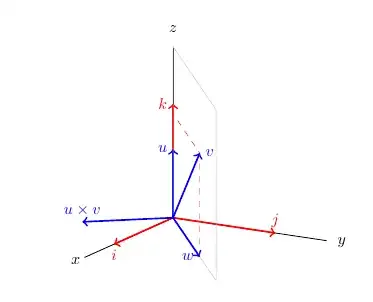
enter image description here

Using tikz-3dplot package. From your example, I understand that v projection on Oxy is w. Everything depends on the two angles, phi and theta, and the norms of u and w. They are defined at the beginning.

The code

\documentclass[11pt, border=10pt]{standalone}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{math, calc}
\begin{document}

\tikzmath{%
  real \f, \t, \uNorm, \wNorm, \bound;
  \f = 40; % phi angle
  \t = 35; % theta angle
  \uNorm = .6;
  \wNorm = 1.3;
  \bound = 1.5;
}
\tikzset{%
  vec/.style={#1, thick, ->}
}


\tdplotsetmaincoords{75}{120}
\begin{tikzpicture}[every node/.style={scale=.7}, scale=2]
  \begin{scope}[tdplot_main_coords]
    \draw[thin] (0, 0, 0) -- (\bound, 0, 0) node[pos=1.1] {$x$};
    \draw[thin] (0, 0, 0) -- (0, \bound, 0) node[pos=1.1] {$y$};
    \draw[thin] (0, 0, 0) -- (0, 0, \bound) node[pos=1.1] {$z$};


\draw[vec=red] (0, 0, 0) -- (1, 0, 0) node[below] {$i$};
\draw[vec=red] (0, 0, 0) -- (0, 1, 0) node[above] {$j$};
\draw[vec=red] (0, 0, 0) -- (0, 0, 1) node[left] {$k$};

\draw[vec=blue] (0, 0, 0) -- (0, 0, \uNorm)
coordinate (u) node[left] {$u$};
\begin{scope}[rotate around z=\f, canvas is zx plane at y=0]
  \draw[very thin, gray!50] (0, 0) rectangle (\bound, 1.4*\bound);
  \draw[vec=blue] (0, 0) -- (0, \wNorm) coordinate (w) node[left] {$w$};
  \draw[vec=blue] (0, 0) -- ({\wNorm*tan(\t)}, \wNorm)
  coordinate (v) node[right] {$v$};
  \draw[red, dashed, very thin] (w) -- (v)
  let \p1 = (v) in -- (\x1, 0);
\end{scope}

%\draw[red, dashed] (v) -- (w);
\draw[vec=blue, rotate around z=\f]
(0, 0, 0) -- (0, -\uNorm*\wNorm, 0)  node[above] {$u\times v$};



\end{scope}


\end{tikzpicture}
\end{document}
Daniel N
  • 5,687
  • Thanks you all for your answers. I'll look at that. @Juan I also need the module: I want the vector u x v – Didier Jun 12 '23 at 10:07
  • Hello. I tried the let \p1= (U), \p2=(V) in order to get the coordinates of (U) and (V) and do the cross product with the usual formulas. But it seems that let \p1= only gives me x and y but not z. How do I get z? – Didier Jun 14 '23 at 09:23
  • You cannot; that's the point! Even if you use three coordinates, say $(a, b, c)$, as soon as you write $A = (a, b, c)$ in TikZ, TikZ transforms them into the coordinates of the corresponding point on the screen. You have access only at those coordinates afterwards. So you need to know the vectors and do the computations using that knowledge and not with the 2-dimensional points living on the screen. – Daniel N Jun 14 '23 at 12:38
  • Thank you for your answer. – Didier Jun 14 '23 at 14:37