0

I am using the FP-package for multiple choice exams with AMC (automatic multiple choice). For randomization I make use of long formulas which sometimes lead to error messages. The reason for these error messages is that the FP-package seems to have problems with the power of negative numbers. It does not matter if e.g. (-5)^2 or pow(2, -5) is used, this always leads to the messages "FP error: Logarithm of negative value!" or "FP error: UPN stack is empty!". Of course the results are wrong.

Surprisingly, I have not found any posting about this wrong behavior. I cannot believe that I am the first to run into these problems. Any idea how to fix this? Attached please find a minimal document and the respective output.

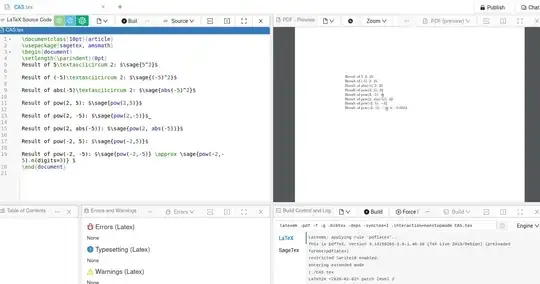
\documentclass[10pt]{article}
\usepackage{fp}
\begin{document}
\setlength{\parindent}{0pt}
\FPeval\Result{5^2}
Result of 5\textasciicircum 2: \Result{} (correct)

\FPeval\Result{(-5)^2}
Result of (-5)\textasciicircum 2: \Result{} (wrong)


\FPeval\Result{abs(-5)^2}
Result of abs(-5)\textasciicircum 2: \Result{} (correct)


\FPeval\Result{pow(2,5)}
Result of pow(2, 5): \Result{} (correct)


\FPeval\Result{pow(2,-5)}
Result of pow(2, -5): \Result{} (wrong)


\FPeval\Result{pow(2,abs(-5))}
Result of pow(2, abs(-5)): \Result{} (correct)


\FPeval\Result{pow(-2,5)}
Result of pow(-2, 5): \Result{} (correct)


\FPeval\Result{pow(-2,-5)}
Result of pow(-2, -5): \Result{} (wrong)


\FPset\myvar{-5}
\FPeval\Result{pow(2,myvar)}
Result of \verb+\FPset\myvar{-5}+ and pow(2, myvar): \Result{} (wrong)
\end{document}

The tex-file results in the following output (FP 0.8 / texlive 2021 / Linux Mint 21.1): enter image description here

JeBa
  • 15
  • 1
    use the xfp package (if using texlive 2021, in a current texlive that is unneeded) and then \fpeval{5**2} \fpeval{(-5)**2} \fpeval{(-5)**(-2)} \fpeval{5**(-2)}. – Ulrike Fischer Jun 23 '23 at 11:56
  • Thanks for the quick answer! Unfortunately, I started using fp because it was suggested by AMC without spending some minutes on searching for an up to date solution. Then I developed a filter with python that converts all quiz questions from Moodle to AMC including all the formulas which now relies on fp. That was quite some effort and and apart from this issue (which can be covered by using abs) everything works fine. But I will definitely spent some time switching with my MoodleToAMC-filter to xfp (sometime in the future). – JeBa Jun 23 '23 at 12:51
  • 1
    If you're already working with external tools why not use them to do the arithmetics? Python should be able to evaluate (−5)² correctly, shouldn't it? – Qrrbrbirlbel Jun 23 '23 at 12:59
  • The documentation doesn't state this, but even \FPeval\Result{pow(2,-1)} results in FP error: UPN stack is empty!. Quite strangely, \FPeval\Result{pow(2,(-1))} gives FP error: Logarithm of negative value!. Apparently, negative exponents are disallowed because of some internal implementation. – egreg Jun 23 '23 at 14:15

2 Answers2

2

I believe it's time to transition to LaTeX3/l3fp which is available in an uptodate distribution without any packages.

Instead of ^, also ** can be used. A pow function isn't provided.

Code

\documentclass[10pt]{article}
\NewDocumentCommand{\FPeval}{mm}{\edef#1{\fpeval{#2}}}
\begin{document}
\setlength{\parindent}{0pt}
\FPeval\Result{5^2}
Result of \verb|5^2|: \Result\ (correct)

\FPeval\Result{(-5)^2}
Result of \verb|(-5)^2|: \Result\ (\textbf{correct})


\FPeval\Result{abs(-5)^2}
Result of \verb|abs(-5)^2|: \Result\ (correct)


\FPeval\Result{(-5)^(-2)}
Result of \verb|(-5)^(-2)|: \Result\ (\textbf{correct})


\FPeval\Result{5^(-2)}
Result of \verb|5^(-2)|: \Result\ (correct)
\end{document}

Output

Result of 5^2: 25 (correct)
Result of (-5)^2: 25 (correct)
Result of abs(-5)^2: 25 (correct)
Result of (-5)^(-2): 0.04 (correct)
Result of 5^(-2): 0.04 (correct)

Qrrbrbirlbel
  • 119,821
  • Also thanks for the quick response! As written as a comment on the posting of Ulrike I am a bit bound to fp at the moment. However, xfp will solve the problem although that means a significant amount of work to switch with my MoodleToAMC filter completely to xfp. – JeBa Jun 23 '23 at 12:54
2

People become aware of limitations when they run into them. For people using little to no math, it's not an issue. You said, "I started using fp because it was suggested by AMC without spending some minutes on searching for an up to date solution". In addition to fp, xfp was suggested as well as LaTeX3/l3fp. You also should be aware of lua for calculations. A post here discusses some of the issues that pop up with the various packages. I'm suggesting a computer algebra system (CAS), even though you have accepted an answer, because I want to make sure you are aware of an up to date solution. SAGE, mentioned in that post, is an open source CAS that is like Mathematica except free. It's website is here. The sagetex package gives you access to Sage as well as Python. Since you said, "I developed a filter with python that converts all quiz questions from Moodle to AMC including all the formulas which now relies on fp." getting access to Python is an extra benefit that you can enjoy in your LaTeX document. Here's a LaTeX document using sagetex for your problem.

\documentclass[10pt]{article}
\usepackage{sagetex, amsmath}
\begin{document}
\setlength{\parindent}{0pt}
Result of 5\textasciicircum 2: $\sage{5^2}$

Result of (-5)\textasciicircum 2: $\sage{(-5)^2}$


Result of abs(-5)\textasciicircum 2: $\sage{abs(-5)^2}$


Result of pow(2, 5): $\sage{pow(2,5)}$


Result of pow(2, -5): $\sage{pow(2,-5)}$


Result of pow(2, abs(-5)): $\sage{pow(2, abs(-5))}$


Result of pow(-2, 5): $\sage{pow(-2,5)}$


Result of pow(-2, -5): $\sage{pow(-2,-5)} \approx \sage{pow(-2,-5).n(digits=3)} $
\end{document}

The output running in Cocalc is below: enter image description here

Some points to notice: first, no set up of the result, just get the answer using \sage{}. That's less typing. Second, notice that sage is giving you the exact answer as a fraction, which is exact, and not a decimal. Finally, notice that I can force SAGE to give you a decimal with \sage{pow(-2,-5).n(digits=3)}; the digits=3 is 3 digits of accuracy. What you can't notice is that SAGE, being a CAS, can handle all sorts of problems (integration, derivatives, matrices, graph theory, etc) without having to reinvent the wheel. My answer to plotting the Weierstrass function here involves Python programming to do the calculation which are then forced through tikz to create the graph. Search this site for sagetex for many other examples of its use.

Given that you use a bit of math and are familiar with Python, you should at look into the sagetex before jumping to LaTeX3/l3fp. Python, a CAS, and LaTeX are a very powerful combination. The drawback to SAGE is that it is not a part of your LaTeX distribution. Therefore it needs to be installed on your computer OR you can sign up for a free Cocalc account.

DJP
  • 12,451