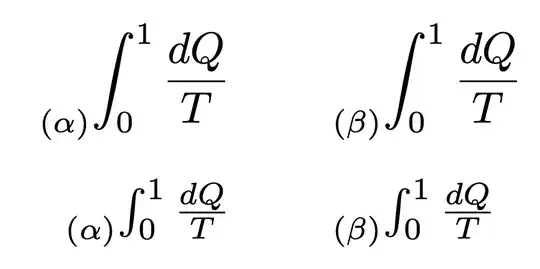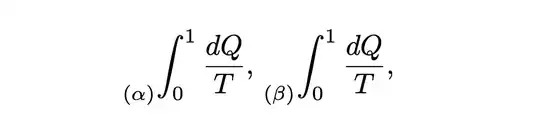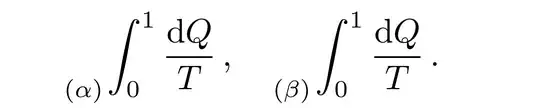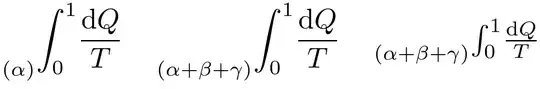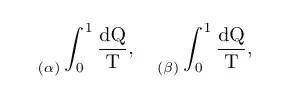Left specification for integral

Question

I am trying to reproduce the following formula, where an integral has a “specification” assigned, placed on its bottom left; any idea on the proper/best way to do so?

Related: https://tex.stackexchange.com/questions/557655/low-level-command-for-controlling-left-superscript-spacing — Gaussler, Jun 26 '23 at 06:08

egreg · Answer 1 · 2023-06-26T09:09:57.447

I set the specification as a subscript to a “phantom” integral. Some care is needed to get spacings right. Since the macro ends with \int, the limits will be read as usual.

\documentclass{article}
\usepackage{amsmath}
\newcommand{\specint}[1]{%
  \mathop{}% for the spacing before the integral
  {\vphantom{\int}}_{(#1)}%
  !% remove the spurious spacing
  \int
}
\begin{document}
[
\specint{\alpha}_0^1\frac{dQ}{T}
\qquad
\specint{\beta}_0^1\frac{dQ}{T}
]
\begin{center}
% to see what happens inline
$\specint{\alpha}_0^1\frac{dQ}{T}
\qquad
\specint{\beta}_0^1\frac{dQ}{T}$
\end{center}
\end{document}

Comparison with the other proposed solutions

\specint is my proposal
\sideset doesn't work inline
with \mathllap the spacing is weird
with \prescript the specification sits lower than the lower limit (and there is no \mathop)
with \raisebox the effect is awful as soon as inline math is tried

\documentclass[twocolumn]{article}
\usepackage{amsmath}
\usepackage{mathtools}
\usepackage[tiny]{titlesec} % spare on vertical spacing
\begin{document}
\section{\texttt{\string\specint}}
\newcommand{\specint}[1]{%
  \mathop{}% for the spacing before the integral
  {\vphantom{\int}}_{(#1)}%
  !% remove the spurious spacing
  \int
}
[
\specint{\alpha}_0^1\frac{dQ}{T}



\specint{\beta}_0^1\frac{dQ}{T}
]
\begin{center}
$\specint{\alpha}_0^1\frac{dQ}{T}



\specint{\beta}_0^1\frac{dQ}{T}$
\end{center}
\section{\texttt{\string\sideset}}
[
\sideset{{(\alpha)}}{^{1}{0}}\int\frac{dQ}{T}



\sideset{{(\beta)}}{^{1}{0}}\int\frac{dQ}{T}
]
\begin{center}
$\sideset{{(\alpha)}}{^{1}{0}}\int\frac{dQ}{T}



\sideset{{(\beta)}}{^{1}{0}}\int\frac{dQ}{T}$
\end{center}
\section{\texttt{\string\mathllap}}
\newcommand\myint[3]{%
   \mkern23mu\int_{\mathllap{(#1)\mkern15mu}#2}^{#3}}
[
\myint{\alpha}{0}{1} \frac{dQ}{T}



\myint{\beta}{0}{1}  \frac{dQ}{T}
]
\begin{center}
$\myint{\alpha}{0}{1} \frac{dQ}{T}



\myint{\beta}{0}{1}  \frac{dQ}{T}$
\end{center}
\newpage
\section{\texttt{\string\prescript}}
[
\prescript{}{(\alpha)}{\int^1_0}\frac{dQ}{T}



\prescript{}{(\beta)}{\int^1_0}\frac{dQ}{T}
]
\begin{center}
$\prescript{}{(\alpha)}{\int^1_0}\frac{dQ}{T}



\prescript{}{(\beta)}{\int^1_0}\frac{dQ}{T}$
\end{center}
\section{\texttt{\string\raisebox}}
[
\raisebox{-.25cm}{$_{(\alpha)}$} \int_0^1 \frac{dQ}{T}



\raisebox{-.25cm}{${(\beta)}$} \int_0^1 \frac{dQ}{T}
]
\begin{center}
$\raisebox{-.25cm}{${(\alpha)}$} \int_0^1 \frac{dQ}{T}



\raisebox{-.25cm}{$_{(\beta)}$} \int_0^1 \frac{dQ}{T}$
\end{center}
\end{document}

@Rpy For your convenience I added a comparison of the proposed solutions — egreg, Jun 26 '23 at 09:10

score 6 · Accepted Answer · answered Jun 25 '23 at 16:56

6

The \sideset command from amsmath is designed for this purpose.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
[
\sideset{{(\alpha)}}{^{1}{0}}\int\frac{dQ}{T},\sideset{{(\beta)}}{^{1}{0}}\int\frac{dQ}{T},
]
\end{document}

answered Jun 25 '23 at 16:56

Sandy G

42,558

That is perfect! Thanks a million! – Rpy Jun 25 '23 at 17:41

Mico · Answer 3 · 2023-06-26T00:05:31.030

I take it that the prefix term -- (\alpha) resp. (\beta) -- and the lower limit of integration -- 0 for both integrals considered here -- must share the same baseline. If this assumption is correct, the following solution, which uses the \mathllap macro provided by the mathtools package (a superset of the amsmath package), should be of interest.

It provides a user-level macro called \myint (feel free to come up with a different name...) that takes three arguments: the prefix, the lower limit of integration, and the upper limit of integration. The first argument should be non-empty -- otherwise, why bother with using \myint? -- while the second and third arguments may be empty.

\documentclass{article}
\usepackage{mathtools} % for \mathllap macro
\newcommand\myint[3]{%
   \mkern23mu\int_{\mathllap{(#1)\mkern15mu}#2}^{#3}}
\begin{document}
[
\myint{\alpha}{0}{1} \frac{\mathrm{d}Q}{T},,
\quad 
\myint{\beta}{0}{1}  \frac{\mathrm{d}Q}{T},.
]
\end{document}

Addendum: As @mbert has pointed out in a comment, the mathtoools package provides a macro called \prescript that's ideally suited to take care of the job at hand.

\documentclass{article}
\usepackage{mathtools} % for '\prescript' macro
\begin{document}
[
\prescript{}{(\alpha)}{\int^1_0}\frac{\mathrm{d}Q}{T}
\quad
\prescript{}{(\alpha+\beta+\gamma)}{\int^1_0}\frac{\mathrm{d}Q}{T}
\quad\textstyle
\prescript{}{(\alpha+\beta+\gamma)}{\int^1_0}\frac{\mathrm{d}Q}{T}
]
\end{document}

mathtools also provides a \prescript command which seems to produce very similar results — mbert, Jun 25 '23 at 17:04
@mbert - Thanks for the suggestion -- I'll post an addendum to show how to use \prescript for the job at hand. — Mico, Jun 26 '23 at 00:02
@egreg - Piece of cake with the help of the \prescript macro. :-) — Mico, Jun 26 '23 at 00:05

score 3 · Answer 4 · answered Jun 25 '23 at 14:43

3

Try this code:

\documentclass{article}
\usepackage{amsmath,adjustbox}
\begin{document}
\[
\raisebox{-.25cm}{$_{(\alpha)}$} \int_0^1 \frac{\text{dQ}}{\text{T}}, \quad \raisebox{-.25cm}{$_{(\beta)}$} \int_0^1 \frac{\text{dQ}}{\text{T}},
\]


\end{document}

Result:

answered Jun 25 '23 at 14:43

Raffaele Santoro

9,702

Just curious: Is there a reason to prefer \raisebox{-.25cm}{$_{(\alpha)}$}\int over \raisebox{-.32cm}{$\scriptstyle(\alpha)$}\int? – Mico Jun 25 '23 at 15:24
@Mico estetic taste... – Raffaele Santoro Jun 25 '23 at 15:34
Thanks for your answer! – Rpy Jun 25 '23 at 17:57

Left specification for integral

4 Answers4

Comparison with the other proposed solutions