Plot a summation of cosine wave

Question

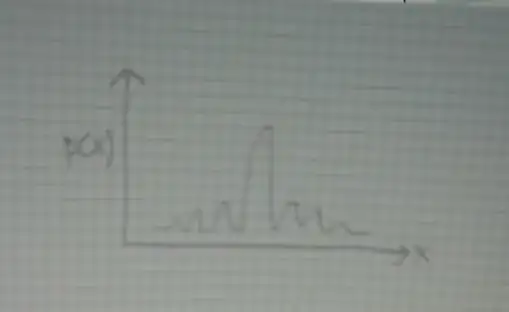
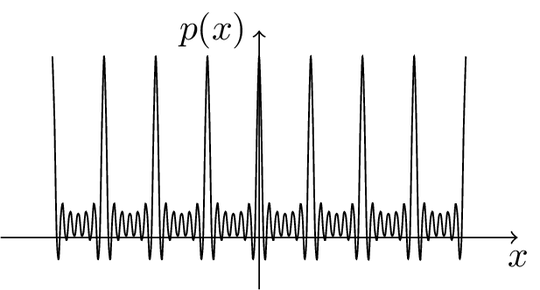
I need to draw a wave that is the summation of these cosine waves

This is my attempt in LuaLaTeX:

\documentclass{article}
\usepackage{pgfplots}
\pgfplotsset{compat=newest}
\usepackage{luacode}
\begin{luacode*}
function p(x)
    assert(x == math.floor(x), "x must be an integer")
    res = 0
    for W = 0, 4000 do
        res = res + (1/2) * (1 + math.cos(2math.pixW))
    end
    tex.sprint(res)
end
\end{luacode}
\begin{document}
\begin{tikzpicture}[
  declare function={p(\n) = \directlua{p(\n)};}
  ]
  \begin{axis}[
    use fpu=false, % very important!
    xlabel=$x$, ylabel=$p(x)$,
    samples at={0,...,21},
    only marks,
    ]
    \addplot {p(x)};
  \end{axis}
\end{tikzpicture}
\end{document}

The shape of the graph I expect held a central absolute maximum, with local maximums that decrease as the central maximum moves away

The graph show nothing

Can you please share your graph, and an expected result? Thx — MS-SPO, Jul 09 '23 at 20:36
Btw, the sum will be larger than infty * (infty + 1) / 4 … or … infty, at least. ? — MS-SPO, Jul 09 '23 at 20:38
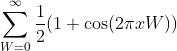
I'm sorry, but your expectation is really wrong here. Split the sums and you get \sum_{0}^{\infty} 0.5 that goes to infty, and then you also have the cosines. (well either your expectation or the formula you show) — Skillmon, Jul 09 '23 at 20:50
And if you only insert integer values for x you're only ever evaluating multiples of 2pi in the cosine, which is 1, and hence you go to infty for that as well. — Skillmon, Jul 09 '23 at 20:55
What you're actually having is a Dirac comb + infty, if I'm not mistaken. — Skillmon, Jul 10 '23 at 19:40
Right, looks like (https://dspillustrations.com/pages/posts/misc/the-dirac-comb-and-its-fourier-transform.html) ... but what's about the question: why does the graph seem to show "nothing" (whatever that may mean) ? — MS-SPO, Jul 10 '23 at 21:09

Gargantuar · Accepted Answer · 2023-07-21T23:15:13.337

I'm still not one of the cool kidz who use LuaLaTeX these days. This solution will be done in plain LaTeX, i.e. pdflatex.

I used the tikzmath library of TikZ, no PGFPlots needed. Also, I don't know whether you really needed the 1+ in the summation, since it will only shift the graph up, but customise the following as you wish. Maybe \n = 6.

\documentclass{standalone}
\usepackage{tikz}
\usetikzlibrary{math}
\begin{document}
\begin{tikzpicture}[scale=.5]
    \tikzmath{
        function f(\x, \n) {
            %\y = \n+1;
            \y = 0;
            for \i in {0,...,\n} {
                \y = \y + cos(deg(2 * pi * \x) * \i);
            };
            \y = \y / 2;
            return \y;
        };
    }
    \draw[->] (-5,0) -- (5,0) node[below] {(x)};
    \draw[->] (0,-1) -- (0,4) node[left] {(p(x))};
    \draw[domain=-4:4, samples=201, smooth] plot (\x, {f(\x,6)});
\end{tikzpicture}
\end{document}

Answer to comment: This should actually work, you only need to add use fpu=false, as you said (see also this question).

\documentclass[convert]{standalone}
\usepackage{tikz}
\usepackage{pgfplots}
\usetikzlibrary{math}
\begin{document}
\begin{tikzpicture}[scale=.5]
    \tikzmath{
        function f(\x, \n) {
            %\y = \n+1;
            \y = 0;
            for \i in {0,...,\n} {
                \y = \y + cos(deg(2 * pi * \x) * \i);
            };
            \y = \y / 2;
            return \y;
        };
    }
    \begin{axis}[use fpu=false]
        \addplot[domain=-4:4, samples=201] {f(x,6)};
    \end{axis}
\end{tikzpicture}
\end{document}

Nice! How can I plot this wave on axis environment? I try \addplot[domain=0:4*pi,samples=200,blue]{{\x, f(\x,20)}}; but doesn't works — user3713179, Jul 21 '23 at 19:29
I've noticed that I made a big but common mistake again: The PGF engine expects the input of cos to be in degrees, not radians (I think this is one of the most dubious features). I will correct this. — Gargantuar, Jul 21 '23 at 21:49
@user3713179 In this sense, OP's drawing was quite misleading. — Gargantuar, Jul 21 '23 at 21:59
One more detail: I changed the number of samples to an odd number since this graph is symmetric in 0. Now the peaks are of even height. — Gargantuar, Jul 21 '23 at 22:22

Plot a summation of cosine wave

1 Answers1