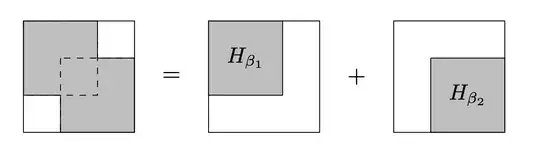
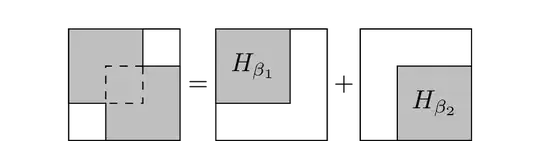How to draw a sparse matrix pattern (using TikZ or not)?

Question

I would like to draw sparsity patterns with overlapping blocks and at the same time be able to write operations in the picture like in the figure below:

Welcome to TeX.SE! Please show us the code you have tried so far! — Mensch, Aug 15 '23 at 16:19
The only tricky bit is the pattern on the left. The problem is that the lines and dashed line need to be added after the squares are filled. You can't just overlap two squares. — John Kormylo, Aug 15 '23 at 16:20
For the left one: 1) draw the big square, filled with gray; 2) draw two white squares on top; 3) draw a square with dashed lines, filled with gray (if needed). With (0,0) to the lower left it's smooth to do with Tikz. — MS-SPO, Aug 15 '23 at 16:56

score 2 · Accepted Answer · answered Aug 15 '23 at 19:40

We'll set up a sparsity diagram style that sets up the appropriate scaling for the xyz coordinate system, draws the big rectangle and also sets up the baseline of the diagrams so that they roughly align with operators.

Then we just draw the rectangles and fill them.

Code

\documentclass{article}
\usepackage{tikz}
\tikzset{
  sparsity diagram/.style={
    execute at begin picture={\draw(0,0)rectangle coordinate (midway) (3,3);},
    x=+5mm, y=+5mm, baseline={([yshift=+-.5ex]midway)}}}
\begin{document}
\[
\tikz[sparsity diagram]{
  \draw[fill=gray!50] (1,0) -| (3,2) -| coordinate (@1)
                      (2,3) -| (0,1) -| coordinate (@2) cycle;
  \draw[dashed] (@1) rectangle (@2);
}
=
\tikz[sparsity diagram]
  \draw[fill=gray!50] (0, 3) rectangle node {$H_{\beta_1}$} + (2,-2);
+
\tikz[sparsity diagram]
  \draw[fill=gray!50] (1, 0) rectangle node {$H_{\beta_2}$}+ (2,2);
\]
\end{document}

Output

There exist better ways to vertically align these squared which are all covered by the answers to Q678914: 1. Using axis_height by the cd library instead of .5ex. 2. Packing the whole diagram into a gathered environment or 3. in a \vcenter{\hbox{…}}. — Qrrbrbirlbel, Aug 15 '23 at 19:56

How to draw a sparse matrix pattern (using TikZ or not)?

1 Answers1

Code

Output