Outlining the boundary of a shape defined by intersections in TikZ

Question

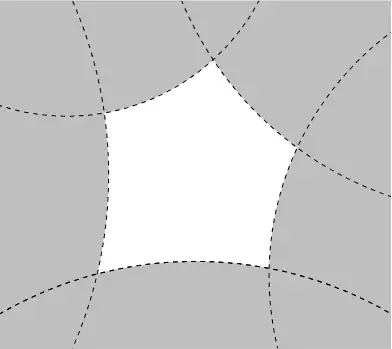
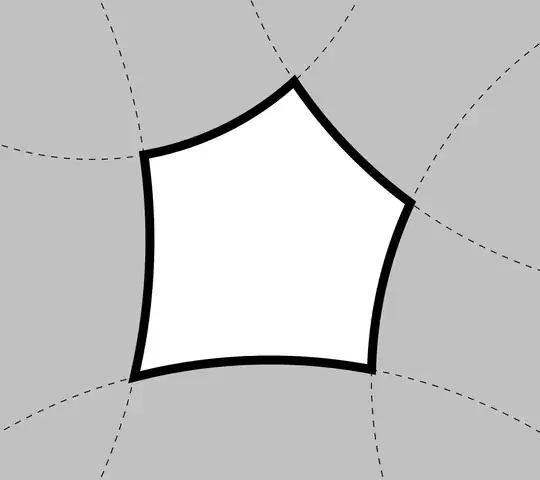
I would like to place a thick border around the white area in the image below, while also maintaining the dashed lines in the gray regions. Is there an easy way to do this?

My code can be found below. Thanks!

\begin{tikzpicture}
\clip (-4.5,-4) rectangle (4.5,4);
\filldrawfill=white rectangle (4.5,4);
\fill[fill=gray!50] (115 : 2 + 5) circle (5);
\fill[fill=gray!50] (45 : 2 + 8) circle (8);
\fill[fill=gray!50] (180 : 2 + 10) circle (10);
\fill[fill=gray!50] (345 : 2 + 7) circle (7);
\fill[fill=gray!50] (270 : 2 + 9) circle (9);
\draw[dashed] (115 : 2 + 5) circle (5);
\draw[dashed] (45 : 2 + 8) circle (8);
\draw[dashed] (180 : 2 + 10) circle (10);
\draw[dashed] (345 : 2 + 7) circle (7);
\draw[dashed] (270 : 2 + 9) circle (9);
\end{tikzpicture}

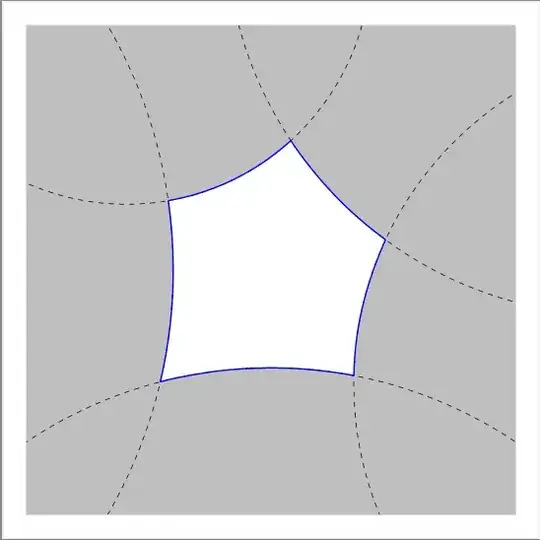
UPDATE:

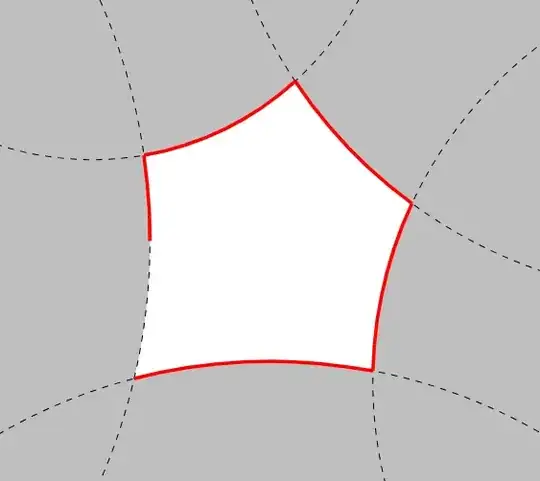
Using the method suggested in Q238967, I've been able to get close, but I am having an issue with one of the lines. I've added the updated code below, along with the new image.

\begin{tikzpicture}
\clip (-4.5,-4) rectangle (4.5,4);
\filldraw[fill=white](-4.5,-4) rectangle (4.5,4);

\fill[fill=gray!50] (45 : 2 + 8) circle (8);
\fill[fill=gray!50] (115 : 2 + 5) circle (5);
\fill[fill=gray!50] (180 : 2 + 10) circle (10);
\fill[fill=gray!50] (270 : 2 + 9) circle (9);    
\fill[fill=gray!50] (345 : 2 + 7) circle (7);


\draw[name path=one, dashed] (45 : 2 + 8) circle (8);
\draw[name path=two, dashed] (115 : 2 + 5) circle (5);
\draw[name path = three, dashed] (180 : 2 + 10) circle (10);
\draw[name path = four, dashed] (270 : 2 + 9) circle (9);
\draw[name path = five, dashed] (345 : 2 + 7) circle (7);


\path[name path = temp1, red, intersection segments={of=one and two,sequence=R2}];
\draw[red,ultra thick, intersection segments={of=temp1 and three,sequence=L3}];

\path[name path = temp2, red, intersection segments={of=one and five,sequence=L1}];
\draw[red,ultra thick, intersection segments={of=temp2 and two,sequence=L3}];

\path[name path = temp3, red, intersection segments={of=four and five,sequence=L3}];
\draw[red,ultra thick, intersection segments={of=temp3 and three, sequence=L1}];

\path[name path = temp4, red, intersection segments={of=three and four,sequence=L1}];
\draw[red,ultra thick, intersection segments={of=temp4 and two, sequence=L1}];

\path[name path = temp5, red, intersection segments={of=one and five,sequence=R3}];
\draw[red,ultra thick, intersection segments={of=temp5 and four, sequence=L1}];



\end{tikzpicture}

Answer 1

You could also do this using the handy buildcycle macro in Metapost, but you need to be careful about how you construct the circles. In particular you need to make sure that you rotate them so that none of the point 0 points lies inside any of the other circles. Purely for comparison, here is my effort:

Compile this with lualatex:

\documentclass[border=5mm]{standalone}
\usepackage{luamplib}
\begin{document}
\mplibtextextlabel{enable}
\begin{mplibcode}
path C[];
C1 = fullcircle scaled 300 rotated 115 shifted 210 dir 115;
C2 = fullcircle scaled 480 rotated  45 shifted 300 dir 45;
C3 = fullcircle scaled 420 rotated 345 shifted 270 dir 345;
C4 = fullcircle scaled 540 rotated 270 shifted 330 dir 270;
C5 = fullcircle scaled 600 rotated 180 shifted 360 dir 180;
path S; S = unitsquare shifted -(1/2,1/2) scaled 300;
for i = 1 upto 5:
  C[i] := C[i] cutbefore S cutafter S;
endfor
path P; P = buildcycle(C1, C2, C3, C4, C5);
beginfig(1);
  fill S withcolor 7/8;
  fill P withcolor 7/8[red, white];
  draw S;
  draw P withpen pencircle scaled 1 withcolor 2/3 red;
  for i=1 upto 5: 
    draw C[i] dashed evenly; 
  endfor
endfig;
\end{mplibcode}
\end{document}

If you want the red line to hide the dashed lines, then move the draw P line after the loop that draws the arcs. And you might not want any of the colour anyway, so something like this might be better:

beginfig(1);
  fill S withcolor 7/8;
  fill P withcolor background;
  draw S;
  for i=1 upto 5: 
    draw C[i] dashed evenly; 
  endfor
  draw P withpen pencircle scaled 1;
endfig;

which would give:

Notes

• the units are PostScript points 28.35 = 1cm

• you can do polar coordinates in MP using the macro dir. The expression dir 100 expands to right rotated 100 and so gives you the <pair> value (sind 100, cosd 100) which will lie on the unit circle. The expression 200 dir 100 scales this point to be the polar coordinate with radius 200bp and angle 100°.

• this works best if you use the default units (PostScript points) because you can write 200 dir 45 directly. You can use cm etc, but you have to write 7 cm * dir 45 which is a bit less elegant.

• Note that in this idiom fullcircle scaled 300 rotated 115 shifted 210 dir 115; the numbers represent points, degrees, points, and degrees, respectively.

Answer 2

The left circle is indeed a trouble maker since internally it is still an arc starting at angle 0 going all around. This will lead to additional segmentations.

Here is my take on this by doing the dashed parts as arcs that are constructed so that this segmentation won't happen. By choosing a tight angle we also only have exactly one intersection point between each pair of circles (now arcs).

With fillbetween I don't see a good solution to have one path with no move to between the segments which is why I'm using line cap = round here to hide that fact. There's inner moveto (which actually seems to be in the /pgf/fill between/ name space) but I don't know how this should be used. The example doesn't even use it.

This is why I provide a spath3 solutions.

After we just split at intersections each pair of path and then remove the first and the third/last segment on each path we are left with five path segments we just need to connect.

In contrast to the fillbetween solution we can actually join the parts so that it will be one continous path. Not only do the joins look good now we can use the whole area that the path contains to fill, shade or pattern it properly.

---

Keep in mind that all circles and arcs are constructed counterclockwise and your circles are enumerated in the same manner. However, this means we have to construct the inner area clockwise which is why the final \draw in both solutions go 4, 3, 2, 1, 0.

And yes, I start counting at 0 because it makes it easier to do modulo operations on the paths (as the spath3 solutions shows).

Code (fillbetween)

\documentclass[tikz]{standalone}
\usepackage{pgfplots}\pgfplotsset{compat=newest}
\usetikzlibrary{pgfplots.fillbetween}
\begin{document}
\begin{tikzpicture}
\clip (-4.5,-4) rectangle (4.5,4);
\foreach \ang/\rad in {45/8, 115/5, 180/10, 270/9, 345/7}
  \fill[gray!50] (\ang:2+\rad) circle[radius=\rad];
\tikzset{
  arc path/.code args={#1/#2/#3}{% ungrouped loop
    \draw[dashed, name path=p#1] ([shift=(#2+135:#3)]#2:2+#3)
      arc[start angle=#2+135, delta angle=90, radius=#3];},
  arc path/.list={0/45/8, 1/115/5, 2/180/10, 3/270/9, 4/345/7},
  split paths/.code 2 args={
    \path[intersection segments={of=p#1 and p#2, sequence=R1}, name path=p#2 on p#1];},
  split paths/.list={01, 12, 23, 34, 40}
}
\draw[ultra thick, line cap=round,
  intersection segments/.list={{of=p4 and p3 on p2, sequence=R2},
                               {of=p3 and p2 on p1, sequence=R2},
                               {of=p2 and p1 on p0, sequence=R2},
                               {of=p1 and p0 on p4, sequence=R2},
                               {of=p0 and p4 on p3, sequence=R2}}];
\end{tikzpicture}
\end{document}

Code (spath3)

\documentclass[tikz]{standalone}
\usetikzlibrary{spath3, intersections}
\newcommand*\NextOf[2]{\pgfintmod{#1+1}{#2}}
%\newcommand*\PrevOf[2]{\pgfintmod{#1-1}{#2}}
\begin{document}
\begin{tikzpicture}
\clip (-4.5,-4) rectangle (4.5,4);
\foreach \ang/\rad in {45/8, 115/5, 180/10, 270/9, 345/7}
  \fill[gray!50] (\ang:2+\rad) circle[radius=\rad];
\tikzset{
  arc path/.code args={#1/#2/#3}{% ungrouped loop
    \draw[dashed, spath/save=p#1] ([shift=(#2+135:#3)]#2:2+#3)
      arc[start angle=#2+135, delta angle=90, radius=#3];},
  arc path/.list={0/45/8, 1/115/5, 2/180/10, 3/270/9, 4/345/7},
  split paths/.style={spath/split at intersections={p#1}{p\NextOf{#1}{5}}},
  split paths/.list={0, ..., 4},
  remove start and end/.style={spath/remove components={p#1}{1, 3}},
  remove start and end/.list={0, ..., 4},
}
\draw[
  line width=1ex,
  spath/append no move/.list={p4, p..., p0},
  spath/adjust and close=current];
\end{tikzpicture}
\end{document}

Output (spath3)

Not clipped

Answer 3

I am not familiar with the spath package but just for fun and free time

An answer extrapolated from the one given by @AndrewStacy --

https://tex.stackexchange.com/a/682553/197451

The originator can please advise

\documentclass[margin=5mm]{standalone}
\usepackage{ pgfplots}
\usetikzlibrary{calc,intersections, fillbetween, spath3}
\begin{document}
\begin{tikzpicture}
\clip (-5,-5) rectangle (5,5);
\filldraw[fill=white](-5,-5) rectangle (5,5);

\fill[fill=gray!50] (45 : 2 + 8) circle (8);
\draw[spath/save=circle8, dashed] (45 : 2 + 8) circle (8);

\fill[fill=gray!50] (115 : 2 + 5) circle (5);
\draw[spath/save=circle5, dashed] (115 : 2 + 5) circle (5);

\fill[fill=gray!50] (180 : 2 + 10) circle (10);
\draw[spath/save=circle10, dashed] (180 : 2 + 10) circle (10);

\fill[fill=gray!50] (270 : 2 + 9) circle (9);    
\draw[spath/save=circle9, dashed] (270 : 2 + 9) circle (9);

\fill[fill=gray!50] (345 : 2 + 7) circle (7);
\draw[spath/save=circle7, dashed] (345 : 2 + 7) circle (7);

%

\tikzset{%
  spath/split at intersections={circle8}{circle5},
    spath/split at intersections={circle5}{circle10},
        spath/split at intersections={circle10}{circle9},
            spath/split at intersections={circle9}{circle7},
                spath/split at intersections={circle7}{circle8},
  spath/get components of={circle8}\cptsA,
    spath/get components of={circle5}\cptsB,
        spath/get components of={circle10}\cptsC,
            spath/get components of={circle9}\cptsD,
                spath/get components of={circle7}\cptsE,
                    spath/get components of={circle8}\cptsF,
}
\draw[
red,
thick,
spath/use=\getComponentOf{\cptsA}{-2},
spath/use={\getComponentOf{\cptsB}{-3}},
spath/use={\getComponentOf{\cptsC}{-2}},
spath/use={\getComponentOf{\cptsD}{-2}},
spath/use={\getComponentOf{\cptsE}{-2}},
spath/use={\getComponentOf{\cptsF}{3}},
];
%
\end{tikzpicture}
\end{document}

output

EDIT

Based on the comments @AndrewStacey to get all the dashed lines visible also

\documentclass[margin=5mm]{standalone}
\usepackage{ pgfplots}
\usetikzlibrary{calc,intersections, fillbetween, spath3}
\begin{document}
\begin{tikzpicture}

    \clip (-5,-5) rectangle (5,5);
    \filldraw[fill=white](-5,-5) rectangle (5,5);

    \fill[fill=gray!50] (45 : 2 + 8) circle (8);
        \fill[fill=gray!50] (115 : 2 + 5) circle (5);
            \fill[fill=gray!50] (180 : 2 + 10) circle (10);
                    \fill[fill=gray!50] (270 : 2 + 9) circle (9);    
                            \fill[fill=gray!50] (345 : 2 + 7) circle (7);

    \draw[spath/save=circle8, dashed] (45 : 2 + 8) circle (8);
        \draw[spath/save=circle5, dashed] (115 : 2 + 5) circle (5);
            \draw[spath/save=circle10, dashed] (180 : 2 + 10) circle (10);
                \draw[spath/save=circle9, dashed] (270 : 2 + 9) circle (9);
                    \draw[spath/save=circle7, dashed] (345 : 2 + 7) circle (7);
    %   
    \tikzset{%
        spath/split at intersections={circle8}{circle5},
        spath/split at intersections={circle5}{circle10},
        spath/split at intersections={circle10}{circle9},
        spath/split at intersections={circle9}{circle7},
        spath/split at intersections={circle7}{circle8},
        spath/get components of={circle8}\cptsA,
        spath/get components of={circle5}\cptsB,
        spath/get components of={circle10}\cptsC,
        spath/get components of={circle9}\cptsD,
        spath/get components of={circle7}\cptsE,
        spath/get components of={circle8}\cptsF,
    }

    \draw[
    blue,
    thick,
    spath/use=\getComponentOf{\cptsA}{-2},
    spath/use={\getComponentOf{\cptsB}{-3}},
    spath/use={\getComponentOf{\cptsC}{-2}},
    spath/use={\getComponentOf{\cptsD}{-2}},
    spath/use={\getComponentOf{\cptsE}{-2}},
    spath/use={\getComponentOf{\cptsF}{3}},
    ];
    %   

\end{tikzpicture}

\end{document}

Output