How to draw such a winding line

Question

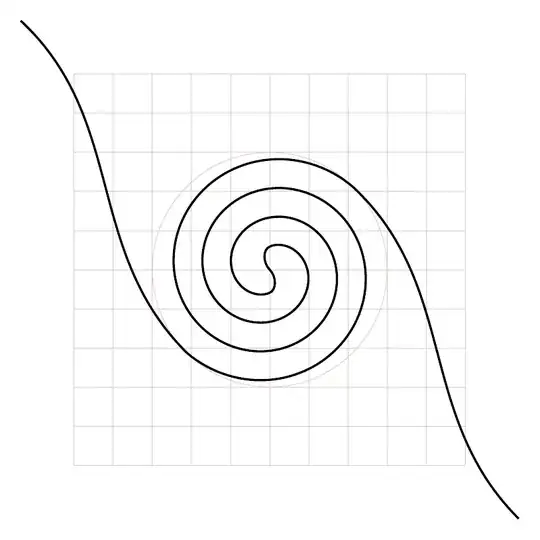
I'm trying to draw a winding line like the solid black one in the following figures using tikz. However, I have no clue how to draw such a complex one.

Could anyone provide some suggestions?

Thanks ahead!

Update: I followed this thread, Spiral spring in TikZ, for generating the two spiral structures. Here is a snipet of my code

\documentclass[tikz,12pt]{standalone}
% the code copied from the attached thread
\newcommand\spiral{}% Just for safety so \def won't overwrite something
\def\spiral#1(#3:#4:#5){% \spiraldraw options(end angle:revolutions:final radius)
\pgfmathsetmacro{\domain}{pi#3/180+#42pi}
\draw [#1,line width=1pt, shift={(#2)}, domain=0:\domain,variable=\t,smooth,samples=int(\domain/0.08)] plot ({\t r}: {#5\t/\domain})
}
\begin{document}
  \begin{tikzpicture}[scale=1]
% plot two spirals
\spiral[black](8,1.6)(0:2:0.6);
\spiral[black](8,1.6)(0:2:-0.6);
\spiral[black](6.86, 1.00)(0:1:0.4);
\spiral[black](6.86, 1.00)(0:1:-0.4);

% connecting them 
\draw[black,line width=1pt] plot [smooth] coordinates {(7.18, 0.81) (7.26, 1) (7.4, 1.6) (7.43, 1.73) (7.48, 1.86)};
\draw[black,line width=1pt] plot [smooth] coordinates {(6.46, 1) (6.37, 0.84) (6.28, 0.69) (6.16, 0.57) (6.01, 0.47) (5.89, 0.41) (5.64, 0.34)};
\draw[black,line width=1pt] plot [smooth] coordinates {(8.6, 1.6) (8.64, 1.84) (8.69, 2.02) (8.77, 2.22)};


\end{tikzpicture}
\end{document}

And here is what I got

To connect the two spirals, I digitized the picture and measured some coordinates, then used these coordinates to draw the lines between them. However, the connections are not smooth.

I know this is a stupid way to do it. Any suggestion for a better way to do this is mostly welcomed!

The small one could be done with Bezier curves easily, the second one is a bit more tricky. — SebGlav, Sep 11 '23 at 20:54
@SebGlav It's exactly the windy, 'twisted' one in the center I'm trying to reproduce. Not the one on the top left. — TurbPhys, Sep 11 '23 at 21:48
Please post a minimal example showing what you've tried. Right now, this is just a do-this-complicated-thing-for-me. — cfr, Sep 11 '23 at 23:08
If you can draw the left curve, the second one could be obtained by "gluing" a similar curve with two spirals. As @cfr says, we need at least one M(merly)WE. — projetmbc, Sep 12 '23 at 07:01
This takes you a considerable way towards your goal - great! There's a package called hobby which can help with drawing smooth curves through points. It's a bit slower, but I think it'd be worth using for something like this where smoothness really matters and is tricky to get right. — cfr, Sep 13 '23 at 21:41
@cfr Then I guess I have to digitize the picture again and get those points? — TurbPhys, Sep 14 '23 at 01:12
The best answer is not always the accepted one or the one with the most votes, especially when answers build on one another and/or some come much later. If you look at the other answer, you'll find the original code you've used gets expanded and parametised. That's easier to work with. In particular, you can get names for the start and end of the spirals. Plugging your numbers from above in, I can recreate the spirals more conveniently. Centring one on the origin will also make things easier. At least, i usually find that's helpful. — cfr, Sep 14 '23 at 01:58
If you name them, you can use the named start and end points to join them. If you fiddle, you could make the transitions smooth. Or you could use the formula and have tikz calculate coordinates to feed to hobby's plot handler and try drawing the two half-spirals and join as a single path. (I tried to do this but I'm an idiot, so mine was a mess. Assuming you're not, yours will be better.) — cfr, Sep 14 '23 at 04:51

score 2 · Answer 1 · answered Sep 15 '23 at 19:22

I do a sketch of the big winding piece of the curve; there are some constants, but you will see, you can not really vary them, except for the radius.

The code

\documentclass[11pt, border=.5cm]{standalone}
\usepackage{tikz}
\usetikzlibrary{math}
\begin{document}
\begin{tikzpicture}[evaluate={%
    \aini = 45;  % initial angle
    \aend = 19;  % 
    \r = 3;  % radius
    \T = 1.5 +.12;  % f\defines the number of turnings of one branch
    \c = .8;
  }]
  \draw[gray!40] (-5, -5) grid (5, 5);
  \draw[red!30] (0, 0) circle (\r);
\draw[black, ultra thick] (-\aini: 3*\r)
  to[out={180 -\aini}, in=-\aini+2] (\aini: \r);
\draw[black, ultra thick, variable=\t, domain=0:\T, samples=200]
  plot (\t360 +\aini: {\r(1 -\c*\t/\T)})
  to[out=\aend, in=-\aini] (-\aini: 0);
\draw[ultra thick, variable=\t, domain=0:\T, samples=200]
  plot (\t360 +\aini +180: {\r(1 -\c*\t/\T)})
  to[out={180 +\aend}, in={180 -\aini}] (180 -\aini: 0);
\draw[ultra thick] (180 -\aini: 3*\r)
  to[out=-\aini+2, in={180 -\aini}] (\aini +180: \r);
\end{tikzpicture}
\end{document}

How to draw such a winding line

1 Answers1