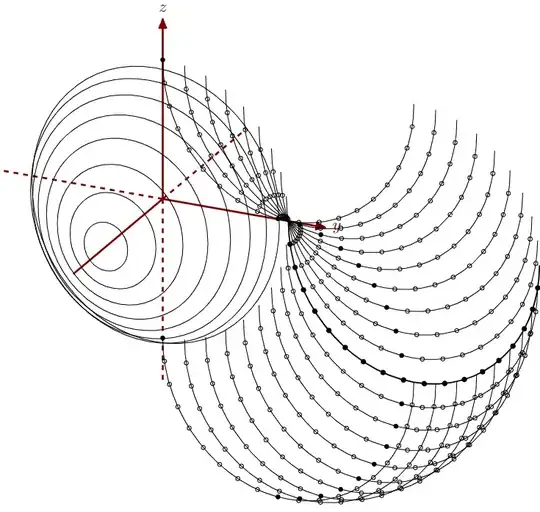
Following the question Half Sphere with lines each 5 degree on the x-axis, I am trying to recreate the figure below:
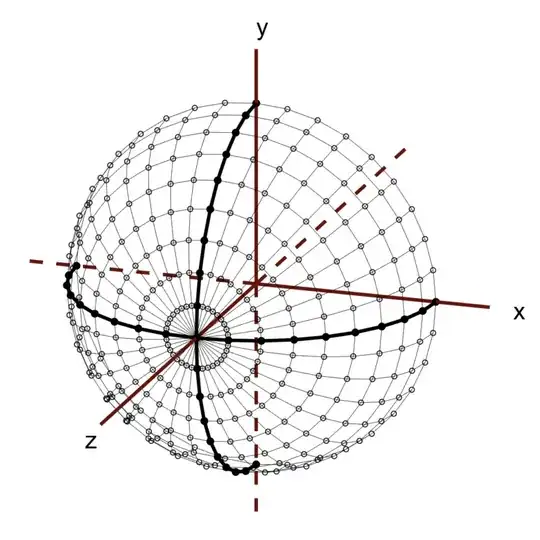
The code I have so far is:
\documentclass[tikz]{standalone}
\usetikzlibrary{arrows.meta, 3d, quotes}
\tikzset{
math nodes/.style={execute at begin node=$, execute at end node=$},
edges/.style={every edge/.append style={#1}}}
\begin{document}
\begin{tikzpicture}[
thin,
> = {Latex [round]},
x = (-10:2.75cm), y = (90:3cm), z = (-140:1.8cm),
axis/.style={very thick, red!50!black},
math nodes, at end,
dot/.style={shape=circle, draw, inner sep=+0pt, minimum size=+2.5pt},
ang 90/.style={thick, nodes=fill, nodes={name=n\pos}},
pos 9/.style=fill
]
\coordinate (O) at (0, 0, 0);
\path[axis, ->] (O) edge["y" right] (1.3, 0, 0 )
edge["z" above] (0, 1.3, 0 ) [-]
edge (0, 0, 1.4 ) [edges=dashed]
edge (-1.3, 0, 0 )
edge ( 0, -1.3, 0 )
edge ( 0, 0, -1.3);
\foreach \ang in {10, 20, ..., 90}
\draw[ang \ang/.try]
(xyz spherical cs: radius=0, latitude=\ang) % start point for arc
[canvas is xy plane at z=\ang/90] % arc is 2d → XY cs in xz plane
circle[start angle=0, delta angle=180, radius=cos \ang];
\foreach \ang in {0, 10, ..., 180}
\draw[ang \ang/.try]
(xyz spherical cs: radius=1, latitude=0, longitude=\ang) % start point for arc
arc[start angle=180, delta angle=180, radius=1]
node foreach \pos in {1, ..., 18} [dot, pos \pos/.try, pos=\pos/19]{};
% Top and bottom nodes (no need to do an arc with radius 0 or place these 18 times)
\node foreach \y in {-1, 1} [dot, pos 9] at (0, \y, 0) {};
% z-axis on top of globe but not on top of dot
path[axis, ->] (n9) edge["x" below left] +(0, 0, 1.4);
\end{tikzpicture}
\end{document}
OUTPUT:
The circles are in place, the arcs start at the correct points, but I'm not sure how to rotate the arcs to achieve the desired output. Any ideas?