to plot the plane of intersection of the sphere $x^2+y^2+z^2=1$ and the plane $x+z=0$

Question

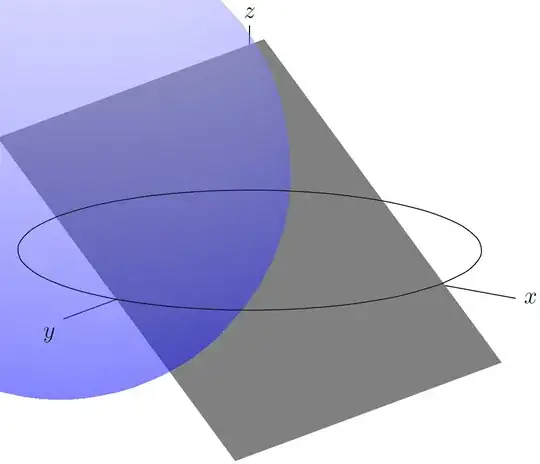
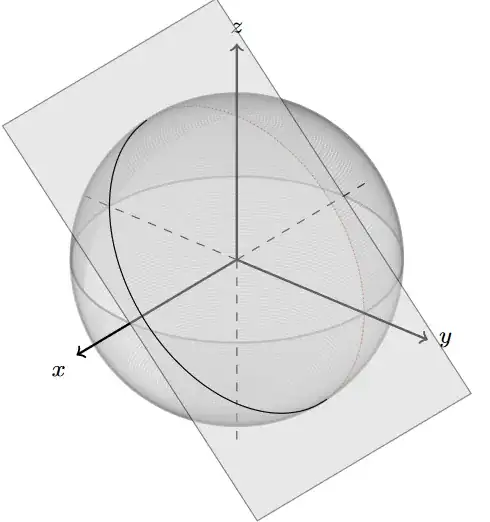
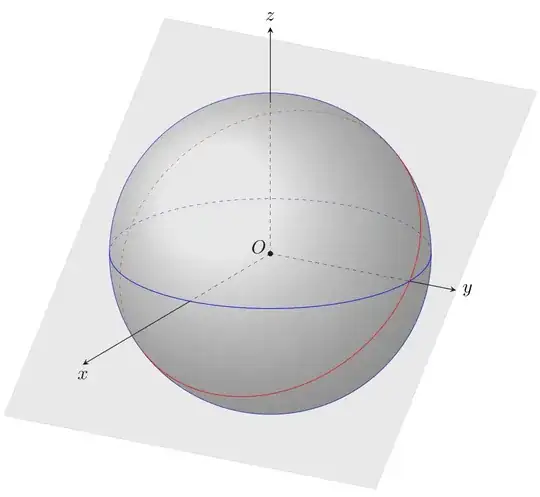
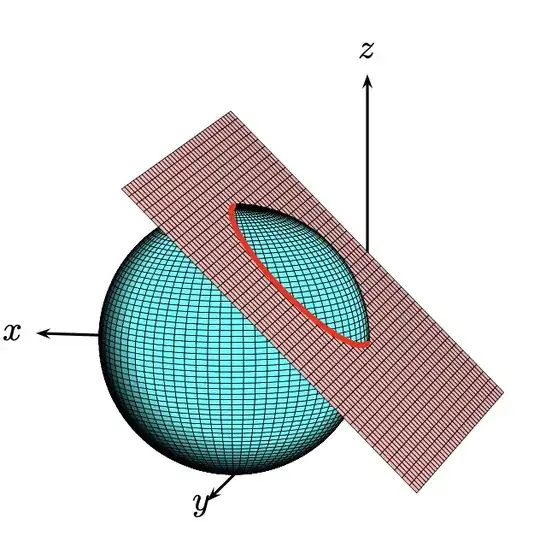
I want to plot the plane of intersection of the sphere $x^2+y^2+z^2=1$ and the plane $x+z=0$.

See the edit

I have tried to plot it with the help of https://tikz.net/parametric-sphere/.

My plane of intersection is not very clearly visible. Also I am not sure where this code is correctly developed.

Please help.

\documentclass[tikz,border=10mm]{standalone}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{math}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{1pt}
%
\begin{document}
    %
    \tdplotsetmaincoords{60}{130}
    \begin{tikzpicture}[tdplot_main_coords]
        % Parametric equations of the sphere
        \tikzmath{function equis(\r,\p,\t) {return \r * sin(\p r) * cos(\t r);};}
        \tikzmath{function ye(\r,\p,\t) {return \r * sin(\p r) * sin(\t r);};}
        \tikzmath{function zeta(\r,\p,\t) {return \r * cos(\p r);};}
        \pgfmathsetmacro{\tcero}{0.0}
        \pgfmathsetmacro{\phiInit}{0.0}
        \pgfmathsetmacro{\phiMid}{0.5*pi}
        \pgfmathsetmacro{\phiEnd}{pi}
        \pgfmathsetmacro{\thetaInit}{0.5*pi}
        \pgfmathsetmacro{\thetaMid}{1.85*pi}
        \pgfmathsetmacro{\thetaEnd}{2.5*pi}
        %
        \pgfmathsetmacro{\step}{0.02}
        \pgfmathsetmacro{\next}{\tcero+0.5*\step}
        \pgfmathsetmacro{\sig}{2.0*\step}
        \pgfmathsetmacro{\radio}{2.0}
        \pgfmathsetmacro{\sigP}{\phiMid+\step}
        \pgfmathsetmacro{\sigPp}{\sigP+\step}
        % Part of the z axis below the sphere
        \draw[dashed] (0,0,-1.25*\radio) -- (0,0,-\radio);
        % I start to draw the sphere from below
        % Part of the sphere under the plane z = 0
        \foreach \p in {\sigP,\sigPp,...,\phiEnd}{          \draw[gray,thick,opacity=0.15] plot[domain=\thetaInit:\thetaEnd,smooth,variable=\t]                 ({equis(\radio,\p,\t)},{ye(\radio,\p,\t)},{zeta(\radio,\p,\t)});        }
        % Then I draw the part of the coordinate axis that is inside the sphere. 
        %%% Coordinate axis
        \draw[thick,->] (0,0,0) -- (1.5*\radio,0,0) node [below left] {\footnotesize$x$};
        \draw[dashed] (0,0,0) -- (-1.25*\radio,0,0);
        \draw[thick,->] (0,0,0) -- (0,1.5*\radio,0) node [right] {\footnotesize$y$};
        \draw[dashed] (0,0,0) -- (0,-1.25*\radio,0);
        \draw[dashed] (0,0,0) -- (0,0,-\radio);
        % As a reference, I draw a circumference at z = 0 (phi = pi / 2).
        \draw[black,thick,opacity=0.25] plot[domain=0:2*pi,smooth,variable=\t]              ({equis(\radio,\phiMid,\t)},{ye(\radio,\phiMid,\t)},{zeta(\radio,\phiMid,\t)});
        % As a reference, I draw a circumference at x = 0 (theta = 0).
        %\draw[red,opacity=0.25] plot[domain=0:2*pi,smooth,variable=\t]     ({equis(\radio,\t,0)},{ye(\radio,\t,0)},{zeta(\radio,\t,0)});
        % As a reference, I draw a circumference at y = 0 (theta = pi/2).
        \draw[red,opacity=0.25] plot[domain=0:2*pi,smooth,variable=\t]              ({equis(\radio,\t,\thetaInit)},{ye(\radio,\t,\thetaInit)},{zeta(\radio,\t,\thetaInit)});
        %
        % Now I draw the part of the sphere that is behind the axis
        %
        \foreach \p in {\step,\sig,...,\phiMid}{
            \draw[gray,thick,opacity=0.25] plot[domain=\thetaInit:\thetaMid,smooth,variable=\t] 
                ({equis(\radio,\p,\t)},{ye(\radio,\p,\t)},{zeta(\radio,\p,\t)}); 
        }
        % Z axis that is inside the sphere
        % This part has to be in front of the rear part of the sphere
        \draw[thick] (0,0,0) -- (0,0,\radio);
  \draw[black,opacity=0.35,densely dotted] plot[domain=-3*pi/4:3*pi/4,smooth,variable=\t]               ({equis(\radio,\t,\thetaInit)},{ye(\radio,\t,\thetaInit)},{zeta(\radio,\t,\thetaInit)});
        %
        % Sphere (the part that is in front of the z axis)
        %
        \foreach \p in {\step,\sig,...,\phiMid}{
            \draw[gray,thick,opacity=0.1] plot[domain=\thetaMid:\thetaEnd,smooth,variable=\t] 
                ({equis(\radio,\p,\t)},{ye(\radio,\p,\t)},{zeta(\radio,\p,\t)}); 
        }
        % Part of the z axis that is above the sphere
        \draw[thick,->] (0,0,\radio) -- (0,0,1.5*\radio) node [above] {\footnotesize$z$};
       \filldraw[
        draw=black,%
        fill=black!20,opacity=0.45%
    ]          (2,2,-2)
            -- (-2,2,-2)
            -- (-2,-2,2)
            -- (2,-2,2)
            -- cycle;
            % As a reference, I draw a circumference at y = 0 (theta = pi/2).
          \draw[black,opacity=0.95] plot[domain=pi/2+pi/4:2*pi-pi/4,smooth,variable=\t]                 ({equis(\radio,\t,\thetaInit)},{ye(\radio,\t,\thetaInit)},{zeta(\radio,\t,\thetaInit)});
    \end{tikzpicture}
\end{document}

Edited

**\documentclass{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\usepgfplotslibrary{fillbetween}
\begin{document}
\begin{tikzpicture} 
  \begin{axis}[
    view={35}{15},
    unit vector ratio=1 1 1,
    ticks = none,
    ymin=-2.8,
    ymax=0,
    xmax=2.8,
    xmin=0,
    zmin=0,
    zmax=2,
    axis lines=middle,
    xlabel=$x$,
    ylabel=$y$,
    zlabel=$z$,
    every axis x label/.style={at={(ticklabel* cs:1)},anchor=west},
    every axis y label/.style={at={(ticklabel* cs:0)},anchor=north east},
    every axis z label/.style={at={(ticklabel* cs:1)},anchor=south},
    x axis line style=-,
    y axis line style=-,
    z axis line style=-,
    clip=false
  ]
\addplot3[name path=toppath,fill=gray, opacity=0.1, fill opacity=0.4,samples=2] (x/4,2,-x/4);
\addplot3[name path=botpath,fill=gray, opacity=0.1, fill opacity=0.4,samples=2] (x/4,-2,-x/4);
\addplot [gray] fill between[of=toppath and botpath];
\addplot3[surf,shader=interp,domain=0:360,y domain=-90:90,opacity=0.5,
    colormap={bluewhite}{color=(blue) color=(blue!30)}] ({2*cos(y)*cos(x)},
    {2*cos(y)*sin(x)},{2*sin(y)});
\addplot3[samples y=0,domain=0:360,smooth]({2*cos(x)},  {2*sin(x)},0);
  \end{axis}
\end{tikzpicture}
\end{document}**

This code is working good but \addplot [gray] fill between[of=toppath and botpath];creats a problem. The sphere slides to the left. Please help.

Answer 1

You can use 3dtools

    \documentclass[border=2mm]{standalone}
    \usepackage{tikz}
    \usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
    \begin{document}
        \begin{tikzpicture}[3d/install view={phi=120,theta=70},line cap=butt,
            line join=round,declare function={R=3;},c/.style={circle,fill,inner sep=1pt}]
            \path
            (0,0,0) coordinate (O)
            ;
        \draw[blue,3d/screen coords] (O) circle[radius=R];
        \shade[ball color=white,3d/screen coords,opacity=0.7] (O) circle[radius=R];
        \path pic[blue]{3d/circle on sphere={R=R,C={(O)}}};
        \path  pic[red]{3d/circle on sphere={R=R, n={(1,0,1)}}}; %(1,0,1) is normal vector of the equation x + z = 0

\draw[3d/hidden] (0,0,0) -- (0,0,R)  (O)--(R,0,0) (O)--(0,R,0);
\draw[3d/visible, -stealth] (R,0,0) -- (R + 4,0,0) node[below]{$x$};
\draw[3d/visible,-stealth] (0,R,0) -- (0,R + 1,0) node[right]{$y$};
\draw[3d/visible, -stealth] (0,0,R) -- (0,0,R + 1.5) node[above]{$z$};
\path foreach \p/\g in {O/150}{(\p)node[c]{}+(\g:2.5mm) node{$\p$}};
\draw[fill=gray,opacity=0.2] (-R,R+1,R) -- (R,R+1,-R) -- (R,-R-1,-R) --(-R,-R-1,R) -- cycle;
    \end{tikzpicture}
    \end{document} 

Answer 2

Run with lualatex, but it needs some time to calculate the intersection:

\documentclass[pstricks]{standalone}
\usepackage{pst-solides3d}
\begin{document}
\begin{pspicture}solidmemory(2,4)
\psset{viewpoint=50 100 10 rtp2xyz,Decran=70,lightsrc=-20 50 20}
\axesIIID(2.5,6,2)
\psSolid[object=plan,definition=equation,args={[-1 0 1 0]},base=-1 2 -2 2,
  ngrid=40 40,fillcolor=red!30,linewidth=0pt,name=B1,action=none]
\psSolidobject=sphere,r=1,fillcolor=cyan,ngrid=72 72,name=C1,action=none
\psSolid[object=fusion,linewidth=0.01pt,base=B1_s C1,linewidth=0.01pt,]
\defFunction[algebraic]{Circle}(t){0.5+0.5cos(t)}{1/sqrt(2)sin(t)}{0.5+0.5*cos(t)}
\psSolid[object=courbe,r=0,function=Circle,range=0 3.14,linecolor=red,linewidth=1.5pt]
\end{pspicture}
\end{document}