Lets say I want to draw a line on a grid given two points A,B:
\documentclass[tikz]{standalone}
%mixing defs and coordinates is a bad idea
\usetikzlibrary{fit,shapes,calc,matrix,math,positioning,arrows.meta}
\begin{document}
\begin{tikzpicture}
\def\xmax{7}
\draw [help lines] (0,0) grid (\xmax,\xmax);
\tikzmath{
coordinate \A, \B;
\A =(1,2);
\B =(4,4);
}
\draw[fill=black] (\A) circle [radius=1pt] node[above,xshift=-1pt] {$A$};
\draw[fill=black] (\B) circle [radius=1pt] node[above,xshift=-1pt] {$B$};
\pgfmathsetmacro{\gradient}{(\By-\Ay)/(\Bx-\Ax)};
\draw (0,\Ay-\gradient*\Ax) -- (\xmax,\Ay-\gradient*\Ax+\gradient*\xmax);
\draw[fill=green] (0,\Ay-\gradient*\Ax) circle [radius=1pt] ;
\draw[fill=red] (\xmax,\Ay-\gradient*\Ax+\gradient*\xmax) circle [radius=1pt] ;
\end{tikzpicture}
\end{document}
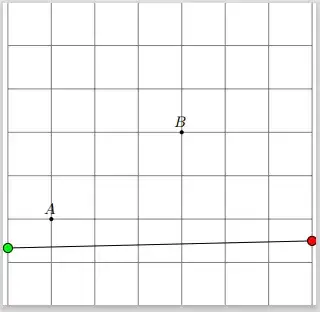
This generates,
which produces a correct left boundary (green dot) but an incorrect right boundary (red dot). It turns out that \Ax and \Ay are not equal to 1cm and 2cm but instead are expressed in pts and
are equal to 28.45274 and 56.90549. Because \gradient is calculated using these units
and the expression for the green dot also uses these units I get the correct result. This is not the case for the red dot since \xmax is definitely not in pts. The result is a y coordinate equal to 42.60365 pt or 1.497348 cm.
Is there a way to avoid this unit mess by forcing the coordinates defined in tikzmath to use the default unit of cm?
\Axto be1,\Ayto be2and then use(\Ax,\Ay)instead of\A(or even define\Ato be\Ax, \Ay) which would allow you to use the\Axand\Aymacros as you wish. – Qrrbrbirlbel Nov 20 '23 at 18:00(intersection of 0,0--0,1 and A--B)which the red one can be found by(intersection of 5,0--5,1 and A--B)(wherex,0--x,1just describes a vertical line with x valuex), this basically does the same math for you. – Qrrbrbirlbel Nov 20 '23 at 18:06\Ay-\gradient*\Ax+\gradient*\xmaxby\Ay-\gradient*\Ax+\gradient*\xmax*1cmand this way clarify that you mean 7cm and not 7pt. – Jasper Habicht Nov 20 '23 at 18:11intersectionmethod. Its good that I have confirmed that it is the default behavior and that there is no way to change the default units of the canvas coordinate system. – Ted Black Nov 20 '23 at 18:40