Inconsistent Arrows When Using Coil

Question

I am trying to produce the below image:

The code I have assembled so far is as follows:

\documentclass[11pt]{book}
\usepackage{amsthm,amssymb}
\usepackage{unicode-math}
\usepackage{tikz}
\usetikzlibrary{arrows.meta,decorations.pathreplacing,decorations.markings}
\usepackage{pgfplots}
\begin{document}
    \begin{figure}
        \centering
        \tikzset{solid node/.style={circle,draw,inner sep=1.2,fill=black},myarrow/.style={scale=1.2,
                decoration={
                    markings,
                    mark=at position 0.3 with {\arrow[scale=1.3]{Latex}}
                },
                postaction={decorate}
            },   myarrow1/.style={
                postaction={
                    decorate,
                    decoration={
                        markings,
                        mark=at position 1 with {\arrow{Latex}}
                    }
                },
                decorate,
                decoration={coil,aspect=0,amplitude=0.8mm,segment length=8mm}
            },
            myarrow2/.style={
                decorate,
                decoration={coil,aspect=0,amplitude=0.6mm,segment length=8mm},
                postaction={
                    decorate,
                    decoration={
                        markings,
                        mark=at position 1 with {\arrow{Latex}}
                    }
                }
            }
        }
        \begin{tikzpicture}
            \node (1) [solid node,label=left:{$1$}] at (0,3){};
            \node (i) [solid node,label=above:{$i$}] at (3,3){};
            \node (j) [solid node,label=left:{$j$}] at (2,0.3){};
            \node (n) [solid node,label=right:{$n$}] at (5,0){};
            \draw[densely dashed,myarrow,bend left=20] (j) to (i);
            \draw[densely dashed,myarrow,bend left=20] (i) to (j);
            \draw[myarrow2] (1) to node[midway, below] {$c$} (i); 
            \draw[myarrow1] (j) to node[midway, below] {$c$} (n); 
        \end{tikzpicture}
    \end{figure}
     \end{document}

Which renders the below image:

As you can observe, the arrows pointing to "i" and "n" look inconsistent with the edges preceding them. That is my first issue. My second issue is that I do not know how I should draw the edge "b" from "i" to "j". Any hint or solution is appreciated.

Some possibilities for the arrow issue here: How to make the arrow more natural?. — Alan Munn, Dec 02 '23 at 17:38
I think it could be possible to create a meta decoration here ... but not sure. I'd just draw the path directly and not use a decoration at all if you want the arrow head to be aligned with the path. You could make use of the sin and cos operators maybe. — Jasper Habicht, Dec 02 '23 at 19:23
@Qrrbrbirlbel I loaded the bending library in the original code. But this being a MWE, I saw that the code would work without it, so I removed it from the piece provided here. — mali1234, Dec 02 '23 at 19:29
@AlanMunn Thanks. I looked into the proposed answer. One of its suggestions was reducing the aspect, which in my case is already 0. The other is lowering the length, which I really cannot do, this being a translation. As for adding post and pre length, it really is not beneficial for the same reason. — mali1234, Dec 02 '23 at 19:48
@mali1234 Yes, I'm not surprised. If you remove the arrow (which is placed via the markings library where bending wouldn't help anyway) you can see that there is a short straight segment at the end because the segment length doesn't fit integer times into the path length. PGF then just fills up the rest with a straight part, and then the arrow is placed at the end of this straight part. It will always look that way then. I think you want a different decoration. (And don't place arrows at position 1.) — Qrrbrbirlbel, Dec 02 '23 at 22:06

Qrrbrbirlbel · Accepted Answer · 2023-12-03T19:49:44.293

If you remove the arrow you can see that there is a short straight segment at the end because the segment length doesn't fit integer times into the path length.

PGF then just fills up the rest with a straight part and then the arrow is placed at the end of this straight part.

I think you want a different decoration. With a slight adjustment it can also be used on a partial path allowing something like

\draw[->]
  (i.30) arc[radius=1, start angle=90+30, delta angle=-200]
  decorate[coily=-.4mm] { -- (j) };

In this example, the delta angle (and thus the end angle) is chosen so that the sine waves are seemingly tangentially to the arc.

Similar things are done for the alternative

\draw[->] (i) 
  (i) to[out=45, in=15, looseness=2] ++(-60:2)
  decorate[coily=-.4mm] { -- (j) };

Also, don't place arrows at position 1. Use the proper arrow tip specification. Then, the bending library's keys flex, flex' and bend also properly work.

Code

\documentclass[tikz]{standalone}
\usepackage{tikz}
\usetikzlibrary{
  arrows.meta, bending, bbox,
  decorations.pathmorphing, decorations.markings}
% decoration complete sines adjusted
% origin: https://tex.stackexchange.com/a/25689
\pgfdeclaredecoration{complete sines}{initial}{
  \state{initial}[
    width=+0pt, next state=sine,
    persistent precomputation=
      \pgfmathsetlength\pgfdecorationsegmentlength{
        \pgfdecoratedinputsegmentlength/
        int(\pgfdecoratedinputsegmentlength/\pgfdecorationsegmentlength)}]{}
  \state{sine}[width=\pgfdecorationsegmentlength]{
    \pgfpathlineto{\pgfpointorigin}
    \pgfpathsine  {\pgfqpoint{0.25\pgfdecorationsegmentlength}{+0.5\pgfdecorationsegmentamplitude}}
    \pgfpathcosine{\pgfqpoint{0.25\pgfdecorationsegmentlength}{-0.5\pgfdecorationsegmentamplitude}}
    \pgfpathsine  {\pgfqpoint{0.25\pgfdecorationsegmentlength}{-0.5\pgfdecorationsegmentamplitude}}
    \pgfpathcosine{\pgfqpoint{0.25\pgfdecorationsegmentlength}{+0.5\pgfdecorationsegmentamplitude}}}
  \state{final}{}}
\tikzset{
  arr/.style={
    postaction=decorate,
    decoration={
      name=markings, mark=at position #1 with {\arrow[scale=1.3]{Latex}}}},
  coily/.style={
    decorate,
    decoration={name=complete sines, amplitude=#1, segment length=6mm}},
  coily1/.style={coily=0.8mm}, coily2/.style={coily=0.6mm}}
\begin{document}
\foreach \bendmode in {quick, flex, bend}{
  \begin{tikzpicture}[
    solid node/.style={shape=circle, draw, inner sep=1.2pt, fill=black},
    > = Latex,
    arrows = {[\bendmode]}
  ]
  \node (1) [solid node, label= left:{$1$}] at (0,3  ) {};
  \node (i) [solid node, label=above:{$i$}] at (3,3  ) {};
  \node (j) [solid node, label= left:{$j$}] at (2,0.3) {};
  \node (n) [solid node, label=right:{$n$}] at (5,0  ) {};
\draw[densely dashed, arr=.3, bend left=20] (j) to (i);
  \draw[densely dashed, arr=.3, bend left=20] (i) to (j);
  \draw[->, coily1] (1) to node[midway, below] {$c$} (i); 
  \draw[->, coily2] (j) to node[midway, below] {$c$} (n); 
  \draw[->] (i) 
   (i.30) arc[radius=1, start angle=90+30, delta angle=-200]
   % or as an alternative something like
%   (i) {[bezier bounding box] to[out=45, in=15, looseness=2] ++(-60:2) }
    node[above]{$b$}
    decorate[coily=-.4mm] { -- (j) };
  \path[sloped] (i) -- node {\bendmode} (j);
  \end{tikzpicture}
}
\end{document}

Output

Brilliant. Do you have any suggestions as to how I should go about drawing the edge "b"? — mali1234, Dec 03 '23 at 04:21

score 2 · Answer 2 · answered Dec 04 '23 at 04:22

Just to have more options, here is a version with decorations.markings, by doing some tricks we can draw a number of repetitions according to the length of the arrow, then we can draw the last marking diferent were the end is almost straight.

RESULT:

MWE:

\documentclass[tikz,border=20pt]{standalone}
\usetikzlibrary{decorations.markings,arrows.meta,calc}
\begin{document}
    \begin{tikzpicture}[
        font=\tiny\sf,
        Nwaves/.store in=\Nwaves,Nwaves=7, %Environment variable for number of waves
        W/.store in=\W,W=0.4, % Variable for amplitude.
        Yscale/.store in=\Yscale,Yscale=1, % Only 1 or -1
        SineArrow/.style={%Decoration definition for SineArrow
            decorate,
            decoration={
                markings,
                mark= between positions 0 and 0.99-1/\Nwaves step 1/\Nwaves %Repeat marking n-1 times
                with {
                    \begin{scope}[yscale=\Yscale]
                        \pgfmathparse{\pgfdecoratedpathlength0.0088/\Nwaves} %0,0088 obtained by tunning
                        \edef\H{\pgfmathresult}
                        \draw[#1,shorten >=0]
                        (0,0)
                            sin (\H,\W/2)
                            cos ++(\H,-\W/2)
                            sin ++(\H,-\W/2)
                            cos ++(\H,\W/2);
                    \end{scope}

                },
                mark= at position 1 % Draw the last marking
                with {
                    \begin{scope}[yscale=\Yscale]
                        \pgfmathparse{\pgfdecoratedpathlength0.0088/\Nwaves}
                        \edef\H{\pgfmathresult}
                        \draw[#1,->]
                        (-4*\H,0)
                            to in=180,out={atan(\H/-\W)+90}, looseness=1.5;% 103 an ofset for arrow orientation.
                    \end{scope}

                }
            }
        },
        solid node/.style={circle,draw,inner sep=1.2,fill=black},
        >={Latex}
    ]
% Start drawing the thing.
% Nodes
\node (1) [solid node,label=left:{$1$}] at (0,3){};
\node (i) [solid node,label=80:$i$] at (3,3){};
\node (j) [solid node,label=left:{$j$}] at (2,0.3){};
\node (n) [solid node,label=right:{$n$}] at (5,0){};

% Arrows
\draw[%Wave Green
    SineArrow=cyan!30!green,
    Nwaves=4,
    W=0.7,
    shorten &gt;= 1pt
](1)
    -- (i.center)
    node[midway, below=3mm]{c};

\draw[blue]
    (j)%Second wave displacement
        to[out=-90+5, in=-180-60] ++(0.1,-0.3)
        coordinate (temp);
\draw[%second wade starting from teportal coordinate
    SineArrow=blue,
    Nwaves=3,
    shorten &gt;= 1pt,
    Yscale=-1,
    W=0.2
](temp)
    -- (n.center)
    node[midway, below=1mm]{c};

%Complementary arrows.  
\draw[dashed,-&gt;](i) to[out=-90+15, in=90-15*3] (j);
\draw[dashed,-&gt;](j) to[out=90+15, in=-90-15*3] (i);
\draw[-&gt;](i)
    to[out=35, in=35, looseness=2] ++(1,-1.5) node[below right]{b}
    to[out=35-180, in=-15](j) ; 
\end{tikzpicture}

\end{document}

Jasper Habicht · Answer 3 · 2023-12-02T19:29:10.073

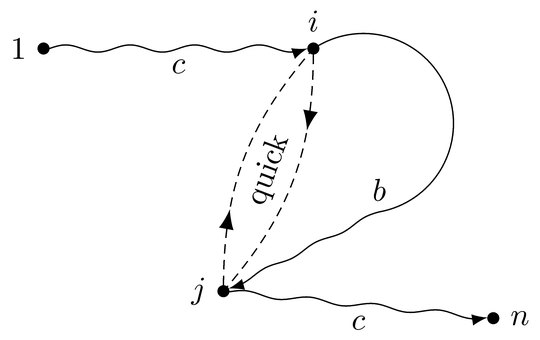
Not really answering the question of how to properly attach arrow heads to decorated paths and probably not the most straight-forward way to solve this, but you could make use of a \pic and draw the paths using the sin and cos operators:

\documentclass[border=10pt]{standalone}
\usepackage{tikz}
\usetikzlibrary{arrows.meta}
\tikzset{
    >={Latex},
    solid node/.style={
        circle,
        fill,
        inner sep=1.25pt,
    },
    pics/sine wave/.style={
        code={
            \tikzset{sine wave/.cd, #1}
            \coordinate[at={\pgfkeysvalueof{/tikz/sine wave/from}}] (-from);
            \coordinate[at={\pgfkeysvalueof{/tikz/sine wave/to}}] (-to);
            \path (-from); \pgfgetlastxy{\startx}{\starty}
            \path (-to); \pgfgetlastxy{\endx}{\endy}
            \pgfmathsetmacro{\currentpathlength}{sqrt((\endx-\startx)^2+(\endy-\starty)^2)}
            \pgfmathsetmacro{\currentpathrotate}{atan2((\endy-\starty),(\endx-\startx))}
            \pgfmathsetmacro{\segmentlength}{\currentpathlength/\pgfkeysvalueof{/tikz/sine wave/frequency}/4}
            \pgfmathsetmacro{\segmentheight}{\pgfkeysvalueof{/tikz/sine wave/amplitude}/2}
            \pgfmathsetmacro{\frequencyint}{int(\pgfkeysvalueof{/tikz/sine wave/frequency})}
            \pgfmathsetmacro{\isinteger}{\pgfkeysvalueof{/tikz/sine wave/frequency}==\frequencyint?1:0)}
            \draw[rotate={\currentpathrotate}, pic actions] (-from) 
                \foreach \n in {1,...,\frequencyint} {
                    sin +({\segmentlength1pt},{\segmentheight}) 
                    cos +({\segmentlength1pt},{-1\segmentheight}) 
                    sin +({\segmentlength1pt},{-1\segmentheight}) 
                    cos +({\segmentlength1pt},{\segmentheight})
                }
                \ifnum\isinteger=1\else
                    sin +({\segmentlength1pt},{\segmentheight}) 
                    cos +({\segmentlength1pt},{-1*\segmentheight}) 
                \fi;
        }
    },
    sine wave/from/.initial={(0,0)},
    sine wave/to/.initial={(1,0)},
    sine wave/frequency/.initial={1},
    sine wave/amplitude/.initial={0.25}
}
\begin{document}
    \begin{tikzpicture}
        \node (1) [solid node,label=left:{$1$}] at (0,3){};
        \node (i) [solid node,label=above:{$i$}] at (3,3){};
        \node (j) [solid node,label=left:{$j$}] at (2,0.3){};
        \node (n) [solid node,label=right:{$n$}] at (5,0){};
        \draw[densely dashed, ->, bend left=20] (j) to (i);
        \draw[densely dashed, ->, bend left=20] (i) to (j);
        \path (1) -- (i) node[midway, below=5pt] {$c$};
        \pic[->] {sine wave={from={(1)}, to={(i)}, frequency={3.5}}};
        \path (j) -- (n) node[midway, below=5pt] {$c$};
        \pic[->] {sine wave={from={(j)}, to={(n)}, frequency={2.5}, amplitude={-0.33}}};
    \end{tikzpicture}
\end{document}

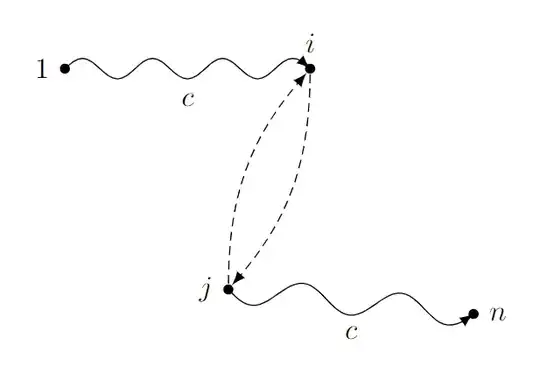
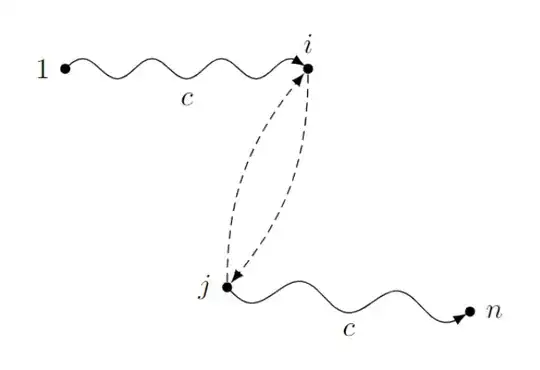
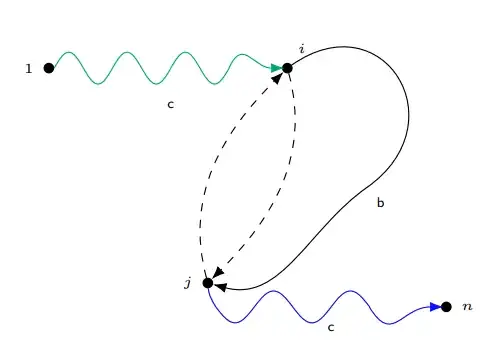
Sadly, this way the arrow heads don't really end at the border of the node shapes. You would need to manually adjust this (as we know the size of the circles due to inner sep=1.25pt, we can use shorten >=1.25pt here). You could also add the bending library to provide for bending arrow heads:

\documentclass[border=10pt]{standalone}
\usepackage{tikz}
\usetikzlibrary{arrows.meta, bending}
\tikzset{
    >={Latex[flex]},
    solid node/.style={
        circle,
        fill,
        inner sep=1.25pt,
    },
    pics/sine wave/.style={
        code={
            \tikzset{sine wave/.cd, #1}
            \coordinate[at={\pgfkeysvalueof{/tikz/sine wave/from}}] (-from);
            \coordinate[at={\pgfkeysvalueof{/tikz/sine wave/to}}] (-to);
            \path (-from); \pgfgetlastxy{\startx}{\starty}
            \path (-to); \pgfgetlastxy{\endx}{\endy}
            \pgfmathsetmacro{\currentpathlength}{sqrt((\endx-\startx)^2+(\endy-\starty)^2)}
            \pgfmathsetmacro{\currentpathrotate}{atan2((\endy-\starty),(\endx-\startx))}
            \pgfmathsetmacro{\segmentlength}{\currentpathlength/\pgfkeysvalueof{/tikz/sine wave/frequency}/4}
            \pgfmathsetmacro{\segmentheight}{\pgfkeysvalueof{/tikz/sine wave/amplitude}/2}
            \pgfmathsetmacro{\frequencyint}{int(\pgfkeysvalueof{/tikz/sine wave/frequency})}
            \pgfmathsetmacro{\isinteger}{\pgfkeysvalueof{/tikz/sine wave/frequency}==\frequencyint?1:0)}
            \draw[rotate={\currentpathrotate}, pic actions] (-from) 
                \foreach \n in {1,...,\frequencyint} {
                    sin +({\segmentlength1pt},{\segmentheight}) 
                    cos +({\segmentlength1pt},{-1\segmentheight}) 
                    sin +({\segmentlength1pt},{-1\segmentheight}) 
                    cos +({\segmentlength1pt},{\segmentheight})
                }
                \ifnum\isinteger=1\else
                    sin +({\segmentlength1pt},{\segmentheight}) 
                    cos +({\segmentlength1pt},{-1*\segmentheight}) 
                \fi;
        }
    },
    sine wave/from/.initial={(0,0)},
    sine wave/to/.initial={(1,0)},
    sine wave/frequency/.initial={1},
    sine wave/amplitude/.initial={0.25}
}
\begin{document}
    \begin{tikzpicture}
        \node (1) [solid node,label=left:{$1$}] at (0,3){};
        \node (i) [solid node,label=above:{$i$}] at (3,3){};
        \node (j) [solid node,label=left:{$j$}] at (2,0.3){};
        \node (n) [solid node,label=right:{$n$}] at (5,0){};
        \draw[densely dashed, ->, bend left=20] (j) to (i);
        \draw[densely dashed, ->, bend left=20] (i) to (j);
        \path (1) -- (i) node[midway, below=5pt] {$c$};
        \pic[->, shorten >=1.25pt] {sine wave={from={(1)}, to={(i)}, frequency={3.5}}};
        \path (j) -- (n) node[midway, below=5pt] {$c$};
        \pic[->, shorten >=1.25pt] {sine wave={from={(j)}, to={(n)}, frequency={2.5}, amplitude={-0.33}}};
    \end{tikzpicture}
\end{document}

Actually, not super nice as the arrow heads don't end at the node shapes border ... well ... it's just an idea anyways. — Jasper Habicht, Dec 02 '23 at 19:25
That's an easy fix if we use the same start and endpoint as the decoration would use. \path (from) -- coordinate[at start] (-from) coordinate[at end] (-to) (to); gives you the points on the border. But then the wave won't "come out" of the nodes. That is just more math to solve, though. — Qrrbrbirlbel, Dec 02 '23 at 19:30
@JasperHabicht That is amazing. How can I learn to code like this? — mali1234, Dec 02 '23 at 19:36

Inconsistent Arrows When Using Coil

3 Answers3

Code

Output