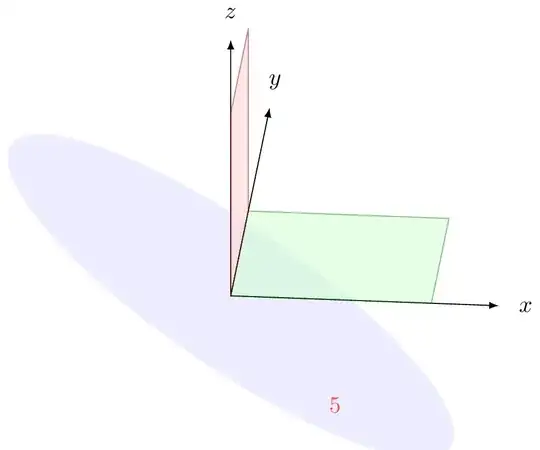
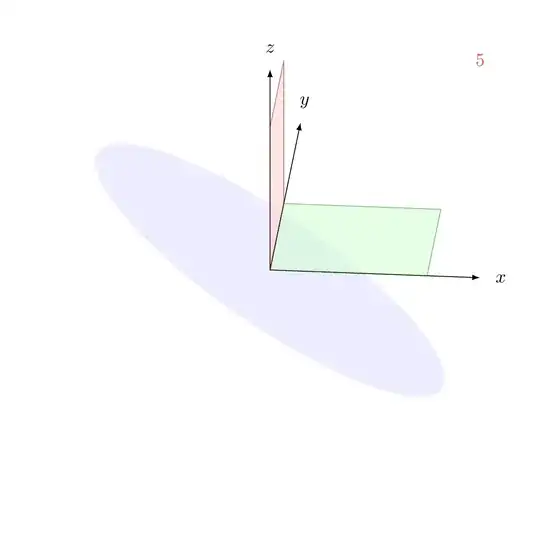
I am trying to pick a good angle to show a plane through the origin and not touching any point in the positive quadrant. Then, I make it into an animation. Is it possible to fix the origin in the animation? Say, the OZ is fixed in every frame of the animation, the origin point is located at the same point on screen.
\documentclass[dvisvgm]{standalone} %for svg
%\documentclass[export]{standalone} %for pdf -> gif
\usepackage{tikz,xcolor}
\usepackage{graphicx}
\usepackage[draft]{animate}
\usetikzlibrary{3d,calc,perspective}
\begin{document}
\newcommand{\BM}[3]{
\def\U{#1} %u
\def\D{#2} %d
\def\R{#3} %R_0
}
\BM{1.2}{0.9}{1.125}
\begin{animateinline}[final,controls={play},loop]{5}
\multiframe{71}{iAngle=5+5}{
%% \foreach \iAngle in {5,10,...,355}{
\begin{tikzpicture}[line cap=round,line join=round,
3d view={\iAngle}{25},
scale=2]
%% \useasboundingbox (-2.5,-2.5) rectangle (3,3);
\pgfmathsetmacro{\gu}{(\R-\D)/(\U-\D)/\R}
\pgfmathsetmacro{\gd}{(\U-\R)/(\U-\D)/\R}
\pgfmathsetmacro{\gg}{1+\gu\gu}
\pgfmathsetmacro{\nu}{1/sqrt(\gg)}
\pgfmathsetmacro{\nd}{\nu/sqrt((\gg+\gd\gd))}
\coordinate (O) at (0,0,0);
\coordinate (X) at (1,0,0);
\coordinate (Y) at (0,1,0);
\coordinate (Z) at (0,0,1);
\coordinate (N) at (\gu,\gd,1);
\coordinate (SPu) at (1,0,-\gu);
\coordinate (SPd) at (0,1,-\gd);
\coordinate (ux) at (1,0,0);
\coordinate (uy) at (0,1,0);
\coordinate (px) at ($\nu(SPu)$);
\coordinate (py) at ($\nd(\gd*\gd,-\gg,\gd)$);
\begin{scope}[red!70, plane origin={(O)},plane x={(px)},
plane y={(py)},canvas is plane]
\filldraw [blue!7!white] (0,0) circle [radius=2];
\node at (1,1) {\iAngle};
%other draws in this plane
\end{scope}
% axes with the desired length
\foreach\i/\j in {X/x,Y/y,Z/z}
{
\draw[-latex] (O) -- ($(\i)!-1cm!(O)$); %Distance Modifiers
\node at ($(\i)!-1.2cm!(O)$) {$\j$};
}
\filldraw[fill=green!20!white, draw=green!50!black, fill opacity=0.5, draw opacity=0.5] (O)
-- ($1.5(ux)$) -- ($1.5(1,1,0)$) -- ($1.5(uy)$) -- cycle;
\filldraw[fill=red!20!white, draw=red!50!black, fill opacity=0.5, draw opacity=0.5] (O)
-- ($1.5(uy)$) -- ($1.5(0,1,1)$) -- ($1.5(0,0,1)$) -- cycle;
%% \draw [blue] (current bounding box.south west) rectangle (current bounding box.north east);
\end{tikzpicture}
}
\end{animateinline}
\end{document}
Here is the output
For this gif file: \documentclass[export]{standalone} to generate pdf, and convert -density 300 -delay 8 -loop 0 -background white out.pdf out.gif