Setting row width in tabular according to the text written inside

Question

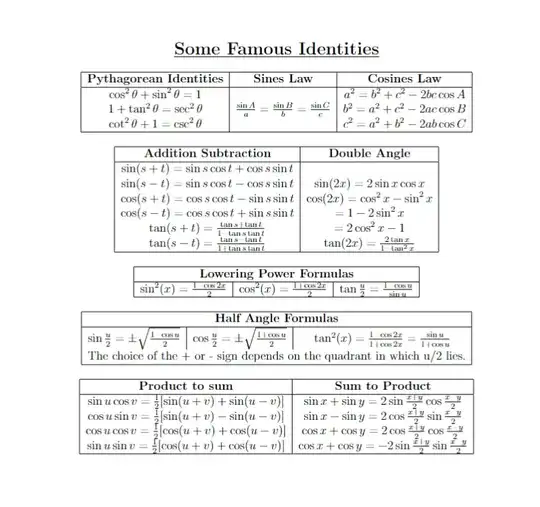
So I am making a formula sheet to provide it to students in the pre-cal exam. But it doesn't look good. It looks conjusted. The output is as follows:

As one can see in the picture, that the first rows in each table, is touching some part of the formula written in second row, also the formulas written in fraction changes the font size, instead, I want it to increase the width when required instead of reducing the font size. Can someone help in that?

here is code for what I have shown in the picture:

\begin{document}
\begin{center}
    \Large{\textbf{\underline{Some Famous Identities}}}
\end{center}
\begin{center}
\begin{tabular}{|c|c|c|}
    \hline
     \bfseries{Pythagorean Identities} & \bfseries{Sines Law} & \bfseries{Cosines Law} \
     \hline
     $\cos^2\theta+\sin^2\theta=1$& & $ a^2 = b^2 + c^2 -2bc \cos{A} $\
     $1 + \tan^2\theta = \sec^2\theta$&$ \frac{\sin{A}}{a} = \frac{\sin{B}}{b} = \frac{\sin{C}}{c} $& $ b^2 = a^2 + c^2 - 2ac \cos{B} $\
     $\cot^2\theta +1=\csc^2\theta$&&$ c^2 = a^2 + b^2 - 2ab \cos{C} $\
     \hline
\end{tabular}
\end{center}
\begin{center}
\begin{tabular}{|c|c|}
    \hline
     \bfseries{Addition Subtraction} &  \bfseries{Double Angle}  \
     \hline
     $\sin(s+t)=\sin{s}\cos{t}+ \cos{s} \sin{t}$& \
     $\sin(s-t)=\sin{s}\cos{t}- \cos{s} \sin{t}$ & $\sin(2x)=2\sin{x}\cos{x}$   \
     $\cos(s+t)=\cos{s}\cos{t}- \sin{s} \sin{t}$ & $\cos(2x)=\cos^2{x}-\sin^2{x}$  \
     $\cos(s-t)=\cos{s}\cos{t}+ \sin{s} \sin{t}$ & $=1-2\sin^2{x}$ \
     $\tan(s+t)=\frac{\tan{s}+ \tan{t}}{1-\tan{s}\tan{t}}$ & $=2\cos^2{x}-1$  \
     $\tan(s-t)=\frac{\tan{s} - \tan{t}}{1+\tan{s}\tan{t}}$    &$\tan(2x)=\frac{2\tan{x}}{1-\tan^2{x}}$ \
     \hline
\end{tabular}
\end{center}
\begin{center}
\begin{tabular}{|c|c|c|}
    \hline
    \multicolumn{3}{|c|}{\bfseries{Lowering Power Formulas}} \
    \hline
   $\sin^2(x)=\frac{1-\cos{2x}}{2}$ & $\cos^2(x)=\frac{1+\cos{2x}}{2}$ & $\tan\frac{u}{2}=\frac{1-\cos{u}}{\sin{u}}$ \
    \hline
  \end{tabular}
\end{center}
\begin{center}
\begin{tabular}{|c|c|c|}
    \hline
    \multicolumn{3}{|c|}{\bfseries{Half Angle Formulas}} \
    \hline
   $\sin\frac{u}{2}=\pm \sqrt{\frac{1-\cos{u}}{2}}$ & $\cos\frac{u}{2}=\pm \sqrt{\frac{1+\cos{u}}{2}}$ & $\tan^2(x)=\frac{1-\cos{2x}}{1+\cos{2x}} =\frac{\sin{u}}{1+\cos{u}}$ \
\multicolumn{3}{|c|}{ The choice of the + or - sign depends on the quadrant in which u/2 lies.} \\
\hline

\end{tabular}

\end{center}
\begin{center}
\begin{tabular}{|c|c|}
     \hline
     \bfseries{Product to sum}& \bfseries{Sum to Product}  \
     \hline
    $\sin{u}\cos{v}=\frac{1}{2}[\sin(u+v)+\sin(u-v)]$ & $\sin{x}+\sin{y}=2\sin\frac{x+y}{2}\cos\frac{x-y}{2}$\
    $\cos{u}\sin{v}=\frac{1}{2}[\sin(u+v)-\sin(u-v)]$ & $\sin{x}-\sin{y}=2\cos\frac{x+y}{2}\sin\frac{x-y}{2}$\
     $\cos{u}\cos{v}=\frac{1}{2}[\cos(u+v)+\cos(u-v)]$ & $\cos{x}+\cos{y}=2\cos\frac{x+y}{2}\cos\frac{x-y}{2}$\
    $\sin{u}\sin{v}=\frac{1}{2}[\cos(u+v)+\cos(u-v)]$ &  $\cos{x}+\cos{y}=-2\sin\frac{x+y}{2}\sin\frac{x-y}{2}$ \
     \hline
\end{tabular}
\end{center}
\end{document}

Answer 1

You can (and should) avoid vertical rules that add nothing to clarity; you also shouldn't try to vertically align unrelated formulas.

\documentclass[a4paper]{article}
\usepackage{amsmath,booktabs,array}
\newcolumntype{C}{>{$\displaystyle}c<{$}}
\newcommand{\splitcell}[1]{%
  \begin{tabular}{@{}C@{}}#1\end{tabular}%
}
\begin{document}
\begin{center}
\Large\textbf{Some Famous Identities}
\end{center}
\begin{center}
\begin{tabular}{@{}CCC@{}}
\toprule
\textbf{Pythagorean Identities} & \textbf{Sine Law} & \textbf{Cosine Law} \
\midrule
\splitcell{
  \cos^2\theta+\sin^2\theta=1 \
  1 + \tan^2\theta = \sec^2\theta \
  \cot^2\theta +1=\csc^2\theta
} &
\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} &
\begin{aligned}
  a^2 &= b^2 + c^2 - 2bc \cos A \
  b^2 &= a^2 + c^2 - 2ac \cos B \
  c^2 &= a^2 + b^2 - 2ab \cos C
\end{aligned} \
\bottomrule
\end{tabular}
\bigskip
\begin{tabular}{@{}CC@{}}
\toprule
\textbf{Addition/Subtraction} &  \textbf{Double Angle} \
\midrule
\begin{aligned}
  \sin(s+t)&=\sin{s}\cos{t}+ \cos{s} \sin{t} \
  \sin(s-t)&=\sin{s}\cos{t}- \cos{s} \sin{t} \ 
  \cos(s+t)&=\cos{s}\cos{t}- \sin{s} \sin{t} \ 
  \cos(s-t)&=\cos{s}\cos{t}+ \sin{s} \sin{t} \
  \addlinespace
  \tan(s+t)&=\frac{\tan{s}+ \tan{t}}{1-\tan{s}\tan{t}} \
  \addlinespace
  \tan(s-t)&=\frac{\tan{s} - \tan{t}}{1+\tan{s}\tan{t}}
\end{aligned} &
\begin{aligned}
  \sin 2x &= 2\sin x\cos x \
  \cos 2x &= \cos^2 x -\sin^2 x  \
          &= 1-2\sin^2 x \
          &= 2\cos^2 x-1  \
  \tan 2x &= \frac{2\tan x}{1-\tan^2 x} \
\end{aligned} \
\addlinespace
\bottomrule
\end{tabular}
\bigskip
\begin{tabular}{@{}CCC@{}}
\toprule
\multicolumn{3}{@{}c@{}}{\textbf{Lowering Power Formulas}} \
\midrule
\sin^2 x=\frac{1-\cos 2x}{2} &
\cos^2 x=\frac{1+\cos 2x}{2} &
\tan^2 x=\frac{1-\cos 2x}{1+\cos 2x}\
\addlinespace
\bottomrule
\end{tabular}
\bigskip
\begin{tabular}{@{}CCC@{}}
\toprule
\multicolumn{3}{@{}c@{}}{\textbf{Half Angle Formulas}} \
\midrule
\biggl\lvert\sin\frac{u}{2}\biggr\rvert = \sqrt{\frac{1-\cos u}{2}} &
\biggl\lvert\cos\frac{u}{2}\biggr\rvert = \sqrt{\frac{1+\cos u}{2}} &
\tan\frac{u}{2}=\frac{1-\cos u}{\sin u} = \frac{\sin u}{1+\cos u} \
\addlinespace
\multicolumn{3}{@{}c@{}}{The choice of the sign depends on the quadrant in which $u/2$ lies.} \
\bottomrule
\end{tabular}
\bigskip
\begin{tabular}{@{}CC@{}}
\toprule
\textbf{Product to sum}& \textbf{Sum to Product} \
\midrule
\sin{u}\cos{v}=\frac{1}{2}[\sin(u+v)+\sin(u-v)] &
  \sin{x}+\sin{y}=2\sin\frac{x+y}{2}\cos\frac{x-y}{2} \
\addlinespace
\cos{u}\sin{v}=\frac{1}{2}[\sin(u+v)-\sin(u-v)] &
  \sin{x}-\sin{y}=2\cos\frac{x+y}{2}\sin\frac{x-y}{2} \
\addlinespace
\cos{u}\cos{v}=\frac{1}{2}[\cos(u+v)+\cos(u-v)] &
  \cos{x}+\cos{y}=2\cos\frac{x+y}{2}\cos\frac{x-y}{2} \
\addlinespace
\sin{u}\sin{v}=\frac{1}{2}[\cos(u+v)+\cos(u-v)] &
  \cos{x}+\cos{y}=-2\sin\frac{x+y}{2}\sin\frac{x-y}{2} \
\addlinespace
\bottomrule
\end{tabular}
\end{center}
\end{document}

<Mathematician hat on>
I'd avoid \pm in the half-angle formulas as the plague. The students have learned that in the quadratic formula \pm means that you choose either branch, whereas here you must take only one. The absolute value avoids any ambiguity.
<Mathematician hat off>

A few other points to note: \Large doesn't take an argument, as well as \sin, \cos and similar. I tried to be consistent with the usage of parentheses.

Answer 2

The tabularray package can be used.

The content is centered by using colspec=ccc.

Horizontal and vertical lines are added with respectively hlines and vlines.

The first row is bold by using row{1}={font=\bfseries}.

The second till the last row are in displaystyle by using row{2-Z}={mode=dmath}.

\documentclass[border=6pt]{standalone}
\usepackage{tabularray}
\begin{document}
\begin{tblr}{
  colspec=ccc,
  hlines,
  vlines,
  row{1}={font=\bfseries},
  row{2-Z}={mode=dmath}
}
Pythagorean Identities & Sines Law & Cosines Law\\
\cos^{2}\theta+\sin^{2}\theta=1 & & a^{2}=b^{2}+c^{2}-2bc\cos A\\
1+\tan^{2}\theta=\sec^{2}\theta & \frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c} & b^{2}=a^{2}+c^{2}-2ac\cos B\\
\cot^{2}\theta+1=\csc^{2}\theta & & c^{2}=a^{2}+b^{2}-2ab\cos C\\
\end{tblr}
\end{document}