I am engaging with the community to seek insights and possible solutions for a LaTeX macro customisation. This is inspired by a discussion in this thread, which explores the possibility of dynamically replacing tokens with control sequences. Specifically, the second answer in the thread provides a foundation for my current approach, aiming to replace arbitrary symbols or words with specified control sequences using the command \myspecdef somethinghere : \somecontrolseq.
Here is the code excerpt from the second answer of the aforementioned thread, demonstrating the initial attempt to create this functionality:
\long\def\isnextchar#1#2#3{\begingroup\toks0={\endgroup#2}\toks1={\endgroup#3}%
\let\tmp=#1\futurelet\next\isnextcharA
}
\def\isnextcharA{\the\toks\ifx\tmp\next0\else1\fi\space}
\def\skipnext#1#2{#1}
\def\trynext#1{\trynextA#1\relax\relax}
\def\trynextA#1#2\relax#3\relax#4#5{%
\ifx\relax#2\relax \def\next{\isnextchar#1{\skipnext{#4}}{#5#3}}\else
\def\next{\isnextchar#1{\skipnext{\trynextA#2\relax#3#1\relax#4{#5}}}{#5#3}}\fi
\next
}
\def\mspecdefA#1#2#3 : #4{\ifx#2\undefined
\def#2{\trynext{#3}#4{#1}}\else
\toks0={\trynext{#3}#4}\toks1=\expandafter{#2}%
\edef#2{\the\toks0{\the\toks1}}\fi
}
\def\mspecdef#1{%
\expandafter\ifx\csname m:#1\endcsname\relax
\expandafter\mathchardef\csname m:#1\endcsname=\mathcode#1 \fi \mathcode#1="8000
\begingroup \lccode~=#1
\lowercase{\endgroup\expandafter\mspecdefA\csname m:#1\endcsname~}%
}
\mspecdef << : \ll
\mspecdef <> : \neq
\mspecdef <= : \leq
\mspecdef <== : \Leftarrow
\mspecdef <=> : \Leftrightarrow
\mspecdef <-- : \leftarrow
\mspecdef <-> : \leftrightarrow
\mspecdef >> : \gg
\mspecdef >= : \geq
\mspecdef --> : \rightarrow
\mspecdef -+ : \pm
\mspecdef +- : \mp
\mspecdef ... : \dots
\mspecdef == : \equiv
\mspecdef =. : \doteq
\mspecdef ==> : \Rightarrow
\mspecdef =( : \subseteq
\mspecdef =) : \supseteq
\mspecdef =[ : \sqsubseteq
\mspecdef =] : \sqsubseteq
\myspecdef integration : \int %<- an example of what I want
\myspecdef int : \int %<- this produces an error whilst...
\myspecdef int : \sin %<- does not!
test:
$$ a << b < c <= d >= e > f >> g $$
$$ a <> b = c =. d == e $$
$$ a <== b <-- c <-> d <=> e --> f ==> g $$
$$ a +- b = -(-a -+ +b) $$
$$ a, ..., z <> a + ...+ z $$
$$ a =( b =) c =[ e =] f $$
[ x^+ ] %<- this produces an error
Although this method allows for dynamic substitution, such as transforming integral into \int, it introduces several issues. Notably, the command causes unexpected brace errors with certain inputs, like \[0^+\] when defining \myspecdef +- : \pm. Whilst an alternate notation \[0^{+}\] resolves this, it is not an ideal requirement. Additionally, the substitution inadvertently affects the tilde ~ character's functionality, leading to errors like missing number, treated as zero. Furthermore, using commands like \operatorname results in 'bad mathchar' errors due to the inclusion of - in the definition.
To address these problems and refine the command's behavior, the fourth answer of the thread offers an alternative approach using expl3 syntax as illustrated below:
\documentclass{article}
\usepackage{amsmath}
\usepackage{xparse}
\ExplSyntaxOn
\seq_new:N \l_math_subs_seq
\cs_new_protected:Npn \math_add_sub:nn #1 #2
{
\seq_put_right:Nn \l_math_subs_seq { { #1 } { #2 } }
}
\cs_new_protected:Npn \math_ascii_sub:n #1
{
\tl_set:Nn \l_tmpa_tl { #1 }
\seq_map_inline:Nn \l_math_subs_seq
{
\tl_replace_all:Nnn \l_tmpa_tl ##1
}
\tl_use:N \l_tmpa_tl
}
\cs_new_protected:Npn \math_grabinline:w #1 $
{
\math_ascii_sub:n { #1 } $
}
\cs_new_protected:Npn \math_grabdisplay:w #1 ]
{
\math_ascii_sub:n { #1 } ]
}
% Set substitutions (be careful with order!)
% Three letter sequences first
\math_add_sub:nn { <== } { \Leftarrow }
\math_add_sub:nn { <=> } { \Leftrightarrow }
\math_add_sub:nn { <-- } { \leftarrow }
\math_add_sub:nn { <-> } { \leftrightarrow }
\math_add_sub:nn { --> } { \rightarrow }
\math_add_sub:nn { ==> } { \Rightarrow }
\math_add_sub:nn { ... } { \dots }
% Then two letter sequences
\math_add_sub:nn { << } { \ll }
\math_add_sub:nn { <> } { \neq }
\math_add_sub:nn { <= } { \leq }
\math_add_sub:nn { >> } { \gg }
\math_add_sub:nn { >= } { \geq }
\math_add_sub:nn { -+ } { \mp }
\math_add_sub:nn { +- } { \pm }
\math_add_sub:nn { == } { \equiv }
\math_add_sub:nn { =. } { \doteq }
\math_add_sub:nn { =( } { \subseteq }
\math_add_sub:nn { =) } { \supseteq }
\math_add_sub:nn { =[ } { \sqsubseteq }
\math_add_sub:nn { =] } { \sqsubseteq }
% Enable substitutions for $...$ and [...]
\everymath { \math_grabinline:w }
\tl_put_right:Nn [ { \math_grabdisplay:w }
\ExplSyntaxOff
\begin{document}
\centering
\newcommand*{\test}[1]{%
$#1$%
[#1]%
}
\test{a << b < c <= d >= e > f >> g}
\test{a <> b = c =. d == e}
\test{a <== b <-- c <-> d <=> e --> f ==> g}
\test{a +- b = -(-a -+ +b)}
\test{a, ..., z <> a + ...+ z}
\test{a =( b =) c =[ e =] f}
\end{document}
While this method seems promising and resolves some issues presented by the initial approach, it has its own limitations. Notably, the order of substitutions significantly affects the outcome, making the solution less flexible and more cumbersome for extensive use. Additionally, I attempted to create an alias for \spec_add_sub:nn using \cs_new_eq:NN \mspecdef \spec_add_sub:nn, but it did not perform as anticipated outside of \ExplSyntaxOn ... \ExplSyntaxOff.
My objective is to refine this LaTeX customization for a more robust and flexible command substitution system, ideally one that can be used conveniently within the document environment, as preamble access might not always be available. I understand that this might be a challenging or unconventional request, but I believe it presents a fascinating problem for the LaTeX community.
I welcome any insights, suggestions, or alternative approaches that could lead to an improved solution. Thank you in advance for your time and assistance.
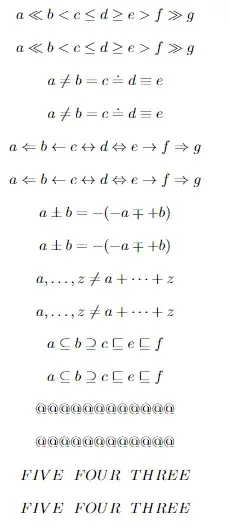
futureletextensively for a letter-by-letter-parser used in thesvgmodule. Provides a Domain Specific Language. For more general solutions Lua is a better option. I have used l3 regex expressions to colorize code in the macrocode environments. – yannisl Dec 25 '23 at 05:39@@is changed to a module name and underscores. But to summarize lpeg and Lua is the way to go for anything more serious. Provide a spec and there are many people here that can help you. – yannisl Dec 25 '23 at 05:39