In the OP's code, the three square root symbols don't have the same height (and depth too, for that matter). IMNSHO, the sum would look a whole lot better if the three square root symbols had the same size. I suggest you change of numerator of the middle term from \mu to \mu\vphantom{2}.

\documentclass{article}
\begin{document}
\[
\sqrt{\frac{2}{\rho}} + \sqrt{\frac{\mu}{\rho}} + \sqrt{\frac{\mu}{2}}
\quad{\mbox{vs.}}\quad
\sqrt{\frac{2}{\rho}} + \sqrt{\frac{\mu\vphantom{2}}{\rho}} + \sqrt{\frac{\mu}{2}}
\]
\end{document}
Addendum: The OP has provided a comment with information about the "real" expression of interest, viz., c_\text{sh}=\sqrt{\frac\mu\rho}, and has asked what kind of placement corrections (if any) I'd apply to this expression.
My main recommendation would be to switch from \frac notation to inline-fraction notation, i.e., to write \sqrt{\mu/\rho}. This works especially well because \mu and \rho happen to have the same height and depth.
If \frac notation cannot be avoided, I'd say that it's the vertical placement of the square root symbol that's the real issue here, rather than the placement of the denominator term in the fraction. Compare \sqrt{\frac{\mu}{\rho}} against \sqrt{\frac{\mu}{\smash[b]{\rho}}}: IMNSHO, the latter expression looks better because while the tall square root symbols have the same overall size in both cases, the square root symbols is placed a bit higher in the latter case, leading to better overall proportions.
Oh, and I'd write c_{\mathrm{sh}} rather than c_{\text{sh}}.
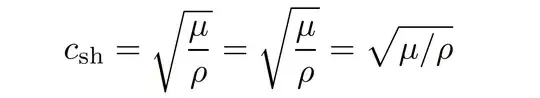
\documentclass{article}
\usepackage{amsmath} % for \smash[b] macro
\begin{document}
\[
c_{\mathrm{sh}}=\sqrt{\frac{\mu}{\rho}}
=\sqrt{\frac{\mu}{\smash[b]{\rho}}}
=\sqrt{\mu/\rho}
\]
\end{document}
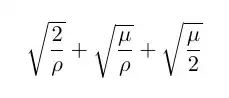
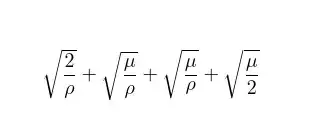

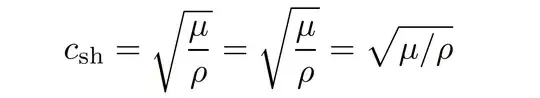
\frac{1}{2}and\frac{1}{}are the same height even though it is all space in the denominator, you see the same in the numerator where the reason for the gap under 2 is to allow y or \mu on the same baseline. So it looks as intended now, I would not change it. – David Carlisle Jan 17 '24 at 12:10\rho^{-1}? – Anna Jan 17 '24 at 12:11c_\text{sh}=\sqrt{\frac\mu\rho}. Do you think adjusting the spacing would make it look like an inconsistent mess even when there's just a single fraction? – Anna Jan 17 '24 at 12:16\muin the numerator that in combination with the large depth of the\rhothat causes this. Maybe you want\sqrt{\frac{\vphantom{2}\mu}{\rho}}? (Since you seem to be fine with the left version.) – mickep Jan 17 '24 at 12:56